Buchberger's algorithm

The Buchberger algorithm ( by Bruno Buchberger ) is in the algebra a method for computing a Gröbner basis of an ideal in a polynomial ring.

The possibility of Gröbner bases to determine algorithmically, many are thus intractable problems, such as the ideal membership problem, or loosening of certain non - linear equations ( as a description of an affine variety), detachable from computer algebra systems.

The Buchberger criterion

It is ...

• A body, and the associated polynomial ring in symbols,
• An ideal,
• A mono murder drying " " given up and
• The generalized polynomial with multiple dividing polynomials defined.

Moreover, that two polynomials

Explained, with the leading term of a polynomial call, ie the respect of the mono murder drying largest monomial together with its coefficients.

The Buchberger criterion then says that a system of generators if and only is a Gröbner basis if all supply through the rest at ( generalized polynomial ) division.

A proof of the Buchberger criterion is in Cox, Little, O'Shea: to find the ideal, Varieties and Algorithms, pp. 84-86.

The algorithm

The Buchberger algorithm can then be formulated as follows.

The idea is that gradually all are formed ( for all pairs of different producers and) that are added to the system of generators of different. With the extended system of generators so the process is repeated, until eventually all disappear; so that the Buchberger criterion is met.

INPUT:   OUTPUT: Gröbner basis   INIT:   1 DO   2   3 FOREACH   4   5 IF THEN   6 NEXT   UNTIL 7 Since the inner loop applies in each run is really so you end up with a system of generators (and not from a larger ideal). The fact that this generating set is a Gröbner basis, then follows from the Buchberger criterion. Note: if and only if it is divided by a Gröbner basis.

If, after the th iteration of the outer loop, the ideal is generated by the Leitmonomen of, we obtain a chain of ideals. Since a chain of ideals can not rise indefinitely ( genuine) (a simple consequence of the Hilbert basis theorem ) has this chain eventually remain constant. This means, however, that from then on no new Leitmonome to be added more; Thus, the algorithm terminates at this point, i.e. after a finite number of steps.

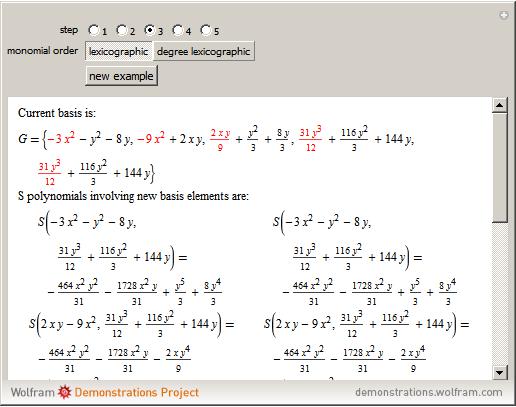
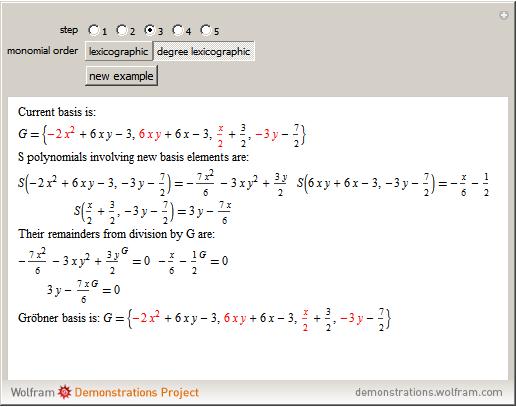
Example

The Gröbner basis, which provides the algorithm quickly becomes very large and thus confusing; moreover, the evaluation of the polynomial divisions is rather complex. Therefore, the algorithm will be presented here only for a very small and simple example are given freely, in the.

Thus, the Buchberger criterion is already fulfilled, after added as producers and the algorithm aborts because no new producers was added to the second pass of the loop.