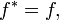CCR and CAR algebras

The CAR- algebra is a considered in the mathematical field of functional analysis, algebra. It is a C * - algebra, which works closely with the studied in quantum mechanics canonical anticommutation (English canonical anticommutation relation, hence the name CAR ) and is therefore also called Fermionenalgebra.

Construction

Refers to the C * - algebra of complex matrices, one can by virtue of an isometric * - homomorphism

Regarded as subalgebra of. On the union of all lying in one another Matrizenalgebren then you have a standard that continues on and so on until all the completeness properties of a C, each of the C * - norms * standard. The completion is then a C * - algebra, called the CAR- algebra.

Canonical anticommutation

Let be a separable Hilbert space and a linear mapping in the C * - algebra of continuous linear operators on the following properties:

For all vectors.

It is said that satisfy the canonical anticommutation; these are met by the creation and annihilation operators considered in the quantum mechanics of fermions. Such maps can be implemented, for example on the Fock space. The isomorphism class of operators generated by the C * - algebra turns out to be independent of the particular choice of the figure, because it is:

• The heat generated by all operators C * - algebra is isomorphic to the CAR algebra.

Is an orthonormal basis of, the embedding can be identified with the above embedding ( here stands for the heat generated from listed in the parentheses operators C * - algebra).

As a UHF Algebra Algebra and AF

Your design according to the CAR- algebra is a UHF - algebra, namely the one for supernatural number ( see the article UHF algebra). As a UHF - algebra, it is also an AF C * - algebra and therefore under all AF C *-algebras distinguished by their parent scaled group. This is represented by the [0,1] range. stands for the set of all rational numbers whose denominator is a power of two.

Product states and type III factors

Each one can recursively define states,

• Is the identity map and
• For each, using as matrix is written with elements of.

Then the restriction of on the same, because, according to the considered here by embedding

.

Therefore, there are at CAR algebra a unique state which matches on all of. This is the name to be associated product state. The term product state is because you can win him over tensor product constructions, but this is not carried out here. According to J. Glimm can be made using these states construct factors of type III as follows.

To state belongs by GNS construction a Hilbert space representation on a Hilbert space. For the image is a C * - algebra whose degree in the weak operator topology is a factor of type III. Two such factors to different numbers from the open interval are not isomorphic.

GICAR algebra

Be a mapping which satisfies the above-defined canonical anticommutation relations. It has, so also satisfies the canonical anticommutation relations, as one can easily recalculate. Since, in both cases, the CAR- algebra is of the or of the generated C * - algebra, where the Hilbert space by running, one can show that one obtains an automorphism, called Eichautomorphismus.

The C * sub- algebra those elements that are invariant among all Eichautomorphismen, is GICAR algebra. It stands for gauge - invariant GI ( German: calibration - invariant ). It can be shown that the GICAR algebra is a AF-C *-algebra. While the CAR- algebra is simple, that is, they have no non-trivial two -sided ideals, the GICAR algebra has a rich ideal structure, which can be read on its Bratteli diagram. This has the form of Pascal's triangle: