Chebyshev's inequality

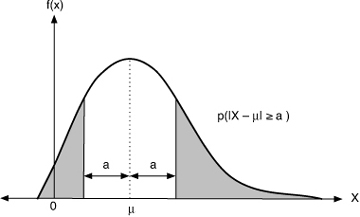
In the Stochastic Chebyshev 's inequality or Chebyshev 's inequality is an inequality that is used for the estimation of probabilities. It is an upper limit for the probability that a random variable with values ​​outside a finite variance located symmetrically around the expected value interval assumes. Thus a lower limit for the probability of it is indicated that the values ​​are within this interval. The set can also be applied to distributions that are either " bell-shaped " nor are symmetrical and sets limits on how much of the data " in the middle" are and how many do not.

The inequality is named in honor of Pafnuti Lvovitch Chebyshev; found in transcriptions occasionally even the spellings Chebyshev or Chebyshev.

• 4.1 Example 1
• 4.2 Example 2
• 4.3 Example 3

Set

Let X be a random variable with mean and finite variance. Then for all real numbers:

By transition to the complementary event is obtained

The proof follows as an application of Markov 's inequality, a simple derivation can also be found below. As one can infer the Markov inequality with school contemporary means of a surface directly insightful comparison and then not derive this version of the Chebyshev inequality, one finds in

The value specified by the Chebyshev inequality constraints can not be improved:

For the discrete random variable with and the equality holds.

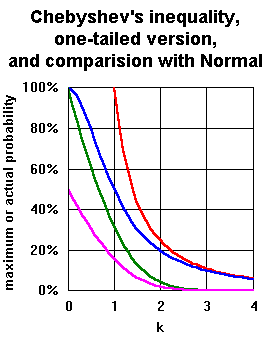
In general, the estimates are rather weak. For example, they are trivial. However, the sentence is often useful because it does not require distributional assumptions on the random variables, and thus for all distributions with finite variance ( especially those that differ greatly from the normal distribution ) is applicable. In addition, the barriers are easy to calculate.

Variants

Deviations expressed by the standard deviation

If the standard deviation is different from zero and a positive number, the result is often quoted with a variant of the Chebyshev inequality:

This inequality provides only for a meaningful assessment for them is trivial, because probabilities are always bounded by 1.

Generalization to higher moments

The Chebyshev inequality can be attributed to higher moments generalize (Lit.: Ash, 1972, Theorem 2.4.9 ): The measure space applies to a measurable function and

This follows from

This yields as a special case of the above inequality by, and sets, because then

Applications

• The phrase is used in the proof of the law of large numbers.
• The generalization to higher torques can be used to show that for the convergence of the convergence function sequences in the level below.
• For the median.

Examples

Example 1

The value for the probability is calculated in the following manner:

Example 2

Another consequence of the theorem is that at least half of the values ​​( ) for each probability distribution with mean and finite standard deviation in the interval.

Example 3

A random event occurs in a model of probability. The experiment is repeated times; the event kick it on time. is then a binomial distribution and has expectation and variance; the relative frequency of occurrence thus has expectation and variance. For the deviation of the relative frequency from the expected value provides the Chebyshev inequality

Where for the second estimate which was used directly from the inequality of the arithmetic and geometric means following relationship.

This formula is the special case of a weak law of large numbers, which shows the stochastic convergence of relative frequencies to the expected value.

The Chebyshev inequality gives for this example only a rough estimate, a quantitative improvement provides the Chernoff inequality.