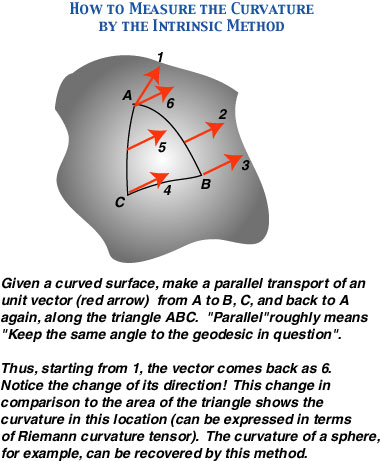
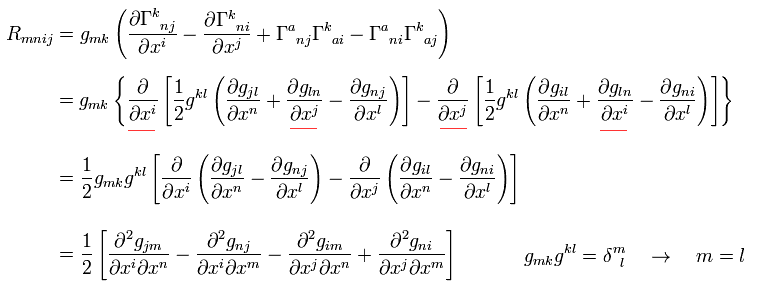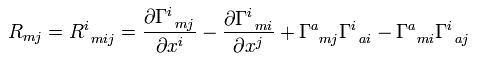Riemann curvature tensor

The Riemannian curvature tensor ( also shorter Riemann tensor, Riemannian curvature or curvature tensor ) describes the curvature of spaces of arbitrary dimension, more specifically Riemannian or pseudo - Riemannian manifolds. It was named after the mathematician Bernhard Riemann and is one of the most important tools of Riemannian geometry. Another important application he is related to the curvature of space- time in general relativity theory.

The Riemann curvature tensor is a tensor of rank 4 you can specify its coefficients, for example in the form. In this article, the Einstein summation convention.

• 3.1 tensor
• 3.2 Symmetries of the curvature tensor
• 3.3 Bianchi identities

• 4.1 Definition
• 4.2 Connecting to the curvature tensor

• 5.1 sectional curvature
• 5.2 Ricci tensor
• 5.3 Krümmungsskalar

Motivation

Diffeomorphisms are the structure-preserving maps between differentiable manifolds and are in accordance with (smooth ) isometries the structure-preserving maps between Riemannian manifolds. Since differentiable manifolds are locally diffeomorphic to the Euclidean space, by definition, the question arose as to whether Riemannian manifolds are locally isometric to. This is not the case. Therefore, the Riemann curvature tensor has been introduced, which, simply put, indicating how locally similar to a Riemannian manifold is the. To better understand the definition of the Riemannian curvature tensor, the following consideration in is prefixed.

Be a vector field. In Euclidean applies to the unit vector fields along the coordinate axes, the equality

Which the set of black backs. Already this is no longer true in general for vector fields. Have in the coordinate representation, the following applies

The term denotes the directional derivative of in direction. On examining now more of the noncommutativity is obtained in Euclidean space

In general manifolds this is wrong. For this reason, the following definition is made ​​.

Definition

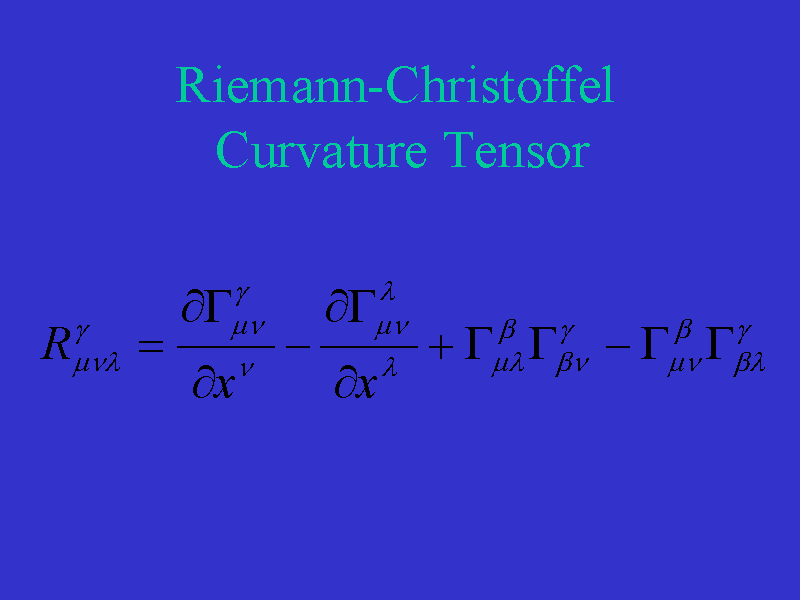
Let be a smooth manifold with the context. Then the Riemannian curvature tensor is a mapping

Which by

Is defined. With the space of smooth vector fields and the Lie bracket is meant.

In local coordinates the curvature tensor can be represented by means of the Christoffel symbols:

Note

Some authors, such as do Carmo or Gallot, Hulin, Lafontaine, which define the Riemann curvature tensor with the opposite sign. In this case, the sign in the definition of sectional curvature and the Ricci curvature of the signs of sectional curvature, Ricci curvature and scalar curvature rotates so that all authors agree.

Properties

Tensor field

The curvature tensor is a tensor -.

• It thus is linear in each variable in particular.
• The value of the manifold at the point depends only on the values ​​of the vector fields, and at the point from (and not on the values ​​in a neighborhood. )

Symmetries of the curvature tensor

On a differentiable manifold with arbitrary context of Kümmungstensor is skew-symmetric in the first two entries, that is, it is

Also applies to Riemannian manifolds with the Levi- Civita connection

• And
• ( " Blockvertauschung ").

Bianchi identities

If a Riemannian manifold with the Levi- Civita connection, then the first Bianchi identity are

And the second Bianchi identity

The first Bianchi identity is also called algebraic Bianchi identity and the second and differential Bianchi identity. Named these identities are named after the mathematician Luigi Bianchi.

Definition

A Riemannian manifold is called flat if it is locally isometric to Euclidean space. This means that for each point there is an environment and a picture, which is isometric, that is true for some. Here denotes the Euclidean scalar product and the Push Forward by.

Connection to the curvature tensor

A Riemannian manifold with Levi- Civita connection if and only flat if the Riemannian curvature tensor is identically zero. Therefore, the developable surface is the two-dimensional analogue of the flat manifold.

Derived quantities

Sectional curvature

One of the main curvature quantities in Riemannian geometry is the sectional curvature. It generalizes the Gaussian curvature of regular surfaces. Here, each level is assigned a curvature in the tangent space at a point of a Riemannian manifold. This is an area in the Gaußkrümmung having a tangential plane and is not curved in the manifold, as it were, a "cut" through the manifold in the direction of the plane. The definition is, however, not with the help of this area, but with the help of the Riemannian curvature tensor and two vectors that span the plane.

Given a Riemannian manifold with Riemannian metric, and a point in a two-dimensional subspace ( plane) of the tangent space of the point. Let and be two tangent vectors that span this plane. with

Is referred to the surface area of the parallelogram and clamped. Then, the size depends

Only of the plane from, but not on the choice of them spanning vectors and. It therefore also writes for and calls this the sectional curvature of.

Is two-dimensional, then there is in every point of just such a two-dimensional subspace of the tangent space, namely the tangent space itself, and is then just the Gaußkrümmung of the point

Ricci tensor

In the Einstein field equations of the so-called Ricci tensor is used (after Gregorio Ricci - Curbastro ). It results from the curvature tensor by Tensorverjüngung:

According to the Einstein summation convention is summed over the same occurring indices, one of which is a above and the other below. For the formation of the Ricci tensor is thus summed over the index. The sign is in this case determined by convention and is in principle arbitrary.

The designation of the indices is arbitrary, it does not matter whether one designates an index with i, j or m. It just depends on its position.

Krümmungsskalar

The Tensorverjüngung of the Ricci tensor is called the Krümmungsskalar (also the Ricci scalar or scalar curvature, formerly Laue scalar). In order to describe its shape will be here first the expression of the Ricci tensor derived:

The Krümmungsskalar derived as follows:, that is, it is summed over the index. Here is the contravariant metric tensor.

The Krümmungsskalar can also be obtained directly from the Ricci tensor:

This is summed over the indices and.