Two's complement

The two's complement (also 2 's complement - b generalized complement ( b basis) - Zweikomplement, B ( Inaer ) complement, Basiskomplement, two's complement ) is a way to represent negative numbers in the binary system. In this case, no additional symbols such as and - are required. This is especially important for computers, which work with bits, which take as values ​​0 or 1. That is, binary numbers are sequences of 0 and 1, the two's complement is the predominant type used to represent the positive and negative numbers in the computer and tapped for arithmetic operations with the help of the calculator.

• 3.1 Addition and Subtraction
• 3.2 sign extension
• 3.3 multiplication

• 5.1 Formal Background to alternative transformations 5.1.1 Separate interpretation of the sign
• 5.1.2 Subtraction of the value range limit

Motivation

As represented by a separate bit in the binary encoding of a negative number which does not exist in the two's complement format, both the sign and the magnitude, it is important to know which bit is used for what. Typically, this is accomplished by removing all numbers have a constant number of digits and are filled as needed with leading zeros, and one of them separate bit encoding the sign. For processing then corresponding control logics are needed that assess the various bits and their meaning.

During the coding in the two's complement on the other hand, the explicit distinction between an excellent sign bit and the bits that describe the amount is not necessary. Negative numbers are indicated by the fact that the most significant bit is set to 1. At 0 there is a positive number or 0. The advantage of this numeral system is that no additional control logic is required for processing in digital circuits.

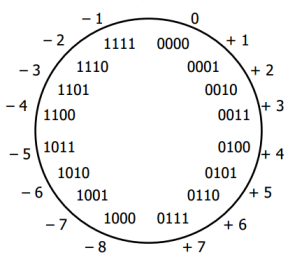
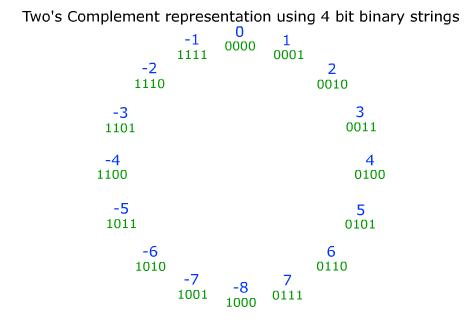
As in the two's complement value of 0 is attributed to the positive numbers, the range of values ​​generally comprises at n binary digits the range ( if not defined otherwise):

Examples:

With 8 bits: 128 ( 10) to 127 (10 ) at 16 bit: -32768 (10 ) to 32767 (10 ) 32 Bit: -2147483648 (10 ) to 2147483647 (10 ) For 64 bits: -9223372036854775808 (10 ) to 9223372036854775807 (10 ) Representation and conversion from the decimal system

The two's complement is required, unlike the one's complement, no case of discriminating whether anticipated negative or positive integers. The problem of the one's complement, to have two representations for zero, does not occur. Positive numbers are provided in the two's complement representation with a leading 0 ( sign bit), and otherwise not changed.

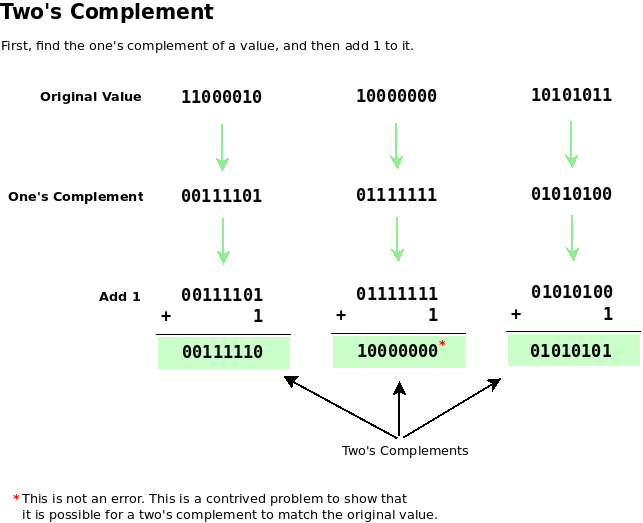
Negative numbers are as follows from a positive number coded: All binary digits are negated and added to the result, the value 1. ( Mathematically accurate method see formal conversion. )

Exemplary conversion of the negative decimal number -4 in the two's complement representation using 8 binary digits:

11111100 (2) = -4 ( 10) Conversion by hand

Trick for faster conversion ( a negative positive in a binary number or vice versa) by hand: starting from the right, write off all zeros and the first one and invert all subsequent digits.

Alternatives

Separate interpretation of the sign

The two's complement can also illustrate this: All the bits have the same value as for a positive representation. The MSB (most significant bit = most significant bit) However, given the negative valence. By subtracting this bit numbers can be converted very quickly. For example 8- bit binary numbers in two's:

00011010 (2) = 16 8 2 = 26 11100110 (2) = -128 64 32 4 2 = -26 In a subsequent section, the accuracy of this method is explained.

Subtraction of the value range limit

Another method you can see the number if it is negative, simply subtract from the number just beyond the range of values ​​. For example, cover unsigned 8 -bit numbers the value range 0-255, directly following number is the 256 A -1 are removed, only 256 and receives the value 255 ( = 1111 1111b ), as desired. Analog performs a -128 to value 128

Interpretation in the residue class ring

For the understanding of the two's, it is helpful to remember that popular microprocessors expect in residue class rings. In fact, it does not go about treating positive and negative numbers differently, but it comes to an agreement which representatives are chosen to describe a certain residue class.

The four basic arithmetic operations in the binary system are identical for positive and negative numbers.

In the context of the previous examples one can consider the bill ( -7 ) * ( -3) on a machine with 8 bit word length. In 8-bit word length is representable number range 0 to 255, and even that is quite a selection of representatives, because it is actually about classes of the residue class ring / 256 And at this point you can choose the numbers from 0 to 255 as representatives, or, completely equivalent, the numbers -128 to 127 using arithmetic in two's complement numbers are, strictly speaking, not " converted ", but are suitable for calculating elected representatives of the residue classes involved.

In the example, the representatives may be chosen 253 and 249 for -3 and -7:

Multiplying the result is:

In the " conversion " from positive to negative numbers, it is really just a clever selection of representatives of the residue classes involved, the special charm of the two's catch the eye: -1 is nothing but the result of the calculation 0 minus one expected in the basic arithmetic operations of the dual system. It is merely added to the 8 bits of a register, as used in this example a carry bit.

Thus, there is the two's complement representation of -1 and the carry bit is set correctly.

One can now interpret the conversion of numbers into two's in the residue class ring. For example, if the preparation of -3 is sought is -3 in the same congruence class as 253 It is therefore sufficient to add to the value of 256 -3 to obtain a usable representative.

When we count the bit positions of the bits 0 to 7 together, this is 255 words Taking 3 as "positive" decimal number and inverts this bit, there is the " value addition " to 255, so 255 - 3 And if I increment the result, this is ( for commutative and associative laws of addition )

The whole bit:

Thus, at the end of the carry bit is set, which indicates a negative number, and the bit sequence 11111101, which corresponds to decimal 253

Further up the text the interpretation of the carry bit has been proposed as -256. This is, incidentally, also at Tietze / Schenck. In fact, we may in the residue class ring / 256 any add on a number often 256 or subtract 256. The congruence is not left. This also applies to integer multiples of 256, so if the carry bit is interpreted as -256, and 1 1 1 1 1 1 1 0 1 therefore as -256 253 = -3 one has actually only the formula 253 = -3 256 different written down.

Arithmetic operations

Addition and subtraction

Addition and subtraction require no case distinction. The subtraction is fed back to an adder.

Examples of 8 bit numbers without sign extension:

-4 3 = -1 corresponds to:    11111100 00000011 = 11111111 4 (- 4) = 0 corresponds to:     00000100 11111100 = 100000000 The front one, in this example, 9 out is discarded.

4 - 3 = 1 corresponds -4 - 3 = -7 corresponds to:     00000100 11111100 11111101 11111101 = 100000001 = 111111001 Here is the correct result by omitting the 9th position, in these cases, one is formed.

As long as the valid n- digit number range in 8 -bit numbers, the value range of the sum of -128 to 127, will not leave, this approach works fine without sign extension. If, however, the range of the sum is outside of the interval, there is an overflow, which is frequently and erroneously confused in this connection with the transfer. The remedy is a sign extension before the arithmetic operation.

Sign extension

Can the two summands have any value, is essential for correctly addition in two's a sign extension necessary. The uppermost point is of two summands first duplicated and thus the number of digits increases by one. In these examples, the point 8, which is copied to the location 9. Subsequently, the addition of as above, but 9 digit is performed. The adder must include one more digit to always.

Differ in the calculated sum then the most significant and the site including each other, the result is not representable in the range of values ​​of the summands - there was an overflow. Depending on the application will then be wider with the one-bit and further expected correct result or an error termination is the result.

For example, the addition of two positive numbers 50 and 80 becomes 130 and so exceeds the range of values. The number still fits in an 8 -bit variable, but the 8th bit is now set so that the number appears incorrectly negative. Some microprocessors such as the 6502 report of such an event with its own status, in this case the overflow bit is O, which queries the programmer according to signed arithmetic operations and can react accordingly.

Example of sign extension, the 9th position of the sign extension is written for clarity in brackets:

4 127 = 131 leads to -4 - 127 = -131 leads to     (0) 00000100 (1) 11111100 (0) 01111111 (1) 10000001     ---------------------- Ü * (0) 11111000 Ü (1) 00000000     ---------------------- = (0) 10000011 = (1) 01111101 * Carry In both cases, the 8th and 9th digit differ, a reduction to 8 bit would result in an error. To illustrate and compare the above two examples with sign extension:

4 - 3 = 1 leads to -4 - 3 = -7 leads to     (0) 00000100 (1) 11111100 ( 1) 11111101 (1) 11111101     ---------------------- Ü (1) 11111000 Ü (1) 11111000     ---------------------- = (0) 00000001 = (1) 11111001 In both cases, the 8 and 9 instead of the sum not differ, the two results can thus be correctly again reduced to 8 digits. In general, the number of digits can be used in two's, starting from the top for so long and without distortion of the value is reduced until the top two places differ from each other in value. This illustrates the fact that in the two's complement representation of numbers is no fixed point for the coding of the sign exists.

Multiplication

The multiplication is possible in the two's complement under Multiplizierwerken and is in particular of digital signal processing a basic operation for the circuit implementation dar. of Multiplizierwerken there are various possibilities. In a parallel multiplier, the product is formed by a sign extension, shift-and- subsequent addition. The individual factors have to be always sign-extended to the product length. In addition to the parallel multipliers and efficient implementation variants of the multiplication which are based on the Booth's algorithm or the bit -pair methods exist.

If there are two factors to each 4 -bit length, the product is 8 bits long. Or in general: For two n-bit and m -bit-wide factors, the product is n m bits long and all factors need to be expanded before the calculation by means of parallel multipliers to this length with the correct sign. At surgery -7 · -3 in two's, which factors can be represented with 4 bits each, is this to be clarified:

11111001 ( decimal equals the number -7, with sign extension )   · 11111101 ( decimal equals the number -3, with sign extension )   ==========   11111001 (1001 · 1, shifted to zero places to the left and with sign extension )   00000000 (1001 · 0, shifted by one position to the left, with sign extension )   11100100 (1001 · 1, shifted two places to the left and with sign extension )   11001000 (1001 · 1, shifted three places to the left, with sign extension )   10010000 (1001 · 1 to four places to the left )   00100000 (1001 · 1 to five places to the left, upper bits postponed )   01000000 (1001 · 1 to six places to the left, upper bits postponed )   10000000 (1001 · 1 to seven digits to the left upper bits postponed )   ==========     00010101 ( decimal equals 21) Because of the sign extension can reduce the number of summands reduce. The reason is that the sign extended up bits of each factor in two's have always identical values. In this example, the sum over the last five lines always provides the negated value of the fourth line, which thus reduces the calculation in this case, the summation of the three rows and the last row and of the subtraction of the half of the above expenses:

1001 ( decimal equals the number -7)       · 1101 ( decimal equals the number -3)       ======   11111001 (1001 · 1, shifted to zero places to the left and with sign extension )   00000000 (1001 · 0, shifted by one position to the left, with sign extension )   11100100 (1001 · 1, shifted two places to the left and with sign extension )   - 11001000 (1001 · 1, shifted three places to the left, with sign extension )   ==========     00010101 ( decimal equals 21) The subtraction in the last line is independent of the signs of the two factors also at other points number and it must be made at the calculated product no sign distinguishing the factors or a sign correction. This subtraction can take place in either full adder circuitry implementations which can be switched into or subtraction. By an inversion of the last line and the additional addition of 1, the same way as in the formation of the two

To illustrate this optimized method multiplying with different signs (-7) · 3 in twos:

1001 ( decimal equals the number -7)       · 0011 ( corresponds to the decimal number 3 )       ======   11111001 (1001 x 1)   11110010 (1001 x 1)   00000000 (1001 · 0 )   - 00000000 (1001 · 0 )   ==========     11101011 ( decimal equals -21) Conversion to decimal

If you want to recode a number of two's complement to decimal, you have to follow (and vice versa according to the conversion from the decimal system in the two's ) proceed:

Example:

11111101 Subtract 1 = 11111100 inverted = 00000011 00000011 in the decimal = 3 3 negative = -3 11111101 ( two's complement ) = -3 ( decimal ) Another approach for converting a number in two's complement in the decimal system is the following: Have the number in two's bodies, so if bits are:

Formal conversion of the binary system

Is a negative number, as calculated in twos () with points as follows:

Accordingly, also applies

Where the positive number represents and acts as a carry in the costs authority in the bill.

Formal background to alternative transformations

Separate interpretation of the sign

The following transformations show that this alternative conversion is correct. If the two's complement of a digit negative number and the suffix of, then the value is calculated as follows:

Here is the interpretation function, which determines the numerical value of a two's complement number. The second line results from the definition of a negative two's complement number, and the third from the conversion to the two's complement of the positive image, wherein the complement to be of. The fourth line then follows from the fact that the complementation as a subtraction from a one- length string () can be represented. The last line corresponds exactly to the alternative conversion rule and therefore shows its correctness.

Subtraction of the value range limit

The correctness of this method is readily apparent when one considers the order in which the numerical values ​​are distributed in the space of bit strings in a bit two's complement number:

That is, by subtracting the number of the limit value range is obtained with account the binary encoding of the two's complement.

Two's complement representation for fixed -point numbers

The two's complement can also be applied to fixed-point numbers, so for example, fractional numbers can be represented as binary. Fixed-point numbers are used, inter alia in the field of digital signal processing. Fixed-point numbers are generally formed by shifting the decimal point, which is located at integers always right behind the last digit. Here, the comma point is not stored in the binary representation, but implicitly assumed his position as a fix, of which the name of the fixed-point representation is derived.

Thus, the above calculation rules, in principle, remain unchanged, only the values ​​change. To form a binary twos complement representation of all binary digits must be inverted and then the value of a quantization 2k added. While k is the position of the last displayable binary digit. In the above integers that would be the point k = 0, which must be added in the formation of Zweikomplements in whole numbers after inversion of the value 20 = 1. Is the decimal point moved, for example, two places to the left and includes the binary word, the two digits to the right of the decimal point would be k = -2, and so must the formation of the two 2-2 = 0.25 are added. ( Note: The decimal point can be located at fixed point numbers outside the representable range of values. )

An example will make this clearer: A binary number with five -bit word length has three integer digits and two decimal places. Thus, the range of values ​​can be represented -4 to 3.75 in steps of 0.25. The number 2.25 corresponds to the binary number 010.012. If now the two's made ​​of all the digits of the binary number are inverted and 2-2 = 0.25 is added, which results in 101.112 = -2.25.

Generalization to other value systems

Also in other important systems can represent integers without using a minus sign. But it has the problem here that the distinction between positive and negative numbers can be agreed more or less arbitrary.

If you limit yourself to - digit numbers to the base, then you can represent integers from 0 to. If one is a number in this area than the largest positive number fixed, then you can interpret any number larger than two's complement representation of the negative number.

The arithmetic operation of negation is carried out analogously as in base 2: Each digit is replaced by, and so the resulting number 1 is added.

For the base and the number of digits obtained for -1 this presentation:

• The numbers of 1, 001
• The negation of the columns gives 443
• Addition of 1 supplies 444

Thus, -1 is represented as 444. The addition 444 001 (base 5 and No. 3) gives 000 as the last transfer is eliminated.

If we take in this example, the largest positive number than 222 fixed (base 5, decimal, this number has the value 62 ), then 223 = -222 is the smallest negative number (decimal -62 ). Thus, the number range is from -62 to 62 in decimal.

For base 10 and No. 2 has 99 = -01 and 50 = -50, here you have so as to base 2 is another number next to 0, which coincides with its two's complement representation. This phenomenon occurs with any straight base.

Generalizing this notation further by allowing infinitely many digits, you get the opportunity to present p- adic integers.