Type I and type II errors#Type II error

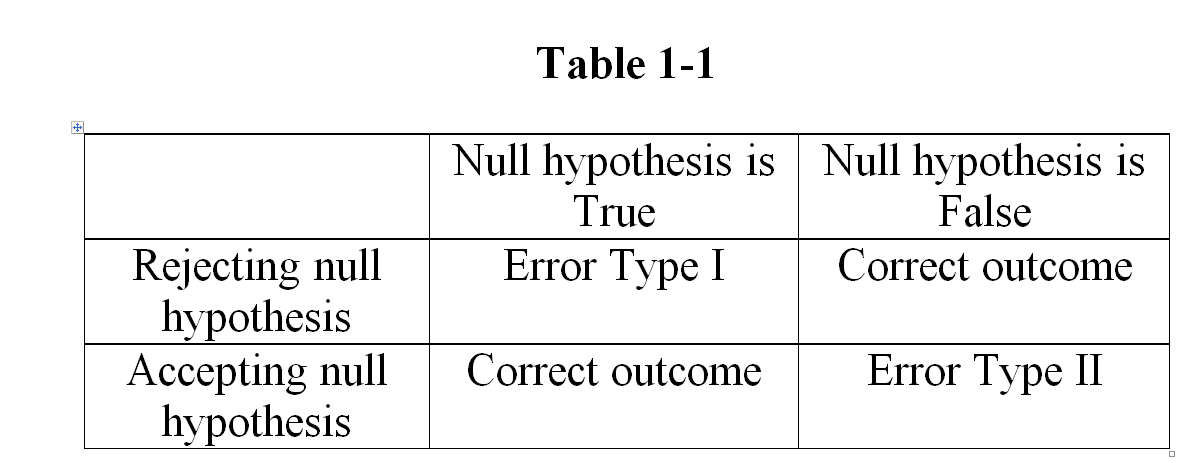
The designated type 2 error, also known as β - error ( beta error) or false negative decision is a technical term in statistics. It refers to a special method of mathematical statistics, the so-called hypothesis testing. When testing a hypothesis, in committing a type 2 error in maintaining the null hypothesis, when in fact the alternative hypothesis is true.

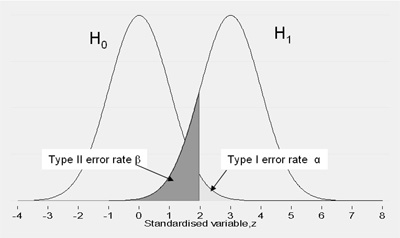
In contrast to the type 1 error, which occurs when the null hypothesis is falsely rejected, the probability of type 2 error can not be calculated mostly. This is due to the nature of the definition of the hypotheses of a statistical test. While the null hypothesis is always a decided statement such as " mean μ = 0 ", mostly global nature of the alternative hypothesis, since they cover all other possibilities (eg " mean μ ≠ 0"). The right graph illustrates the probability of error type 2 (red) μ depending on the unknown population mean.

Decision table

Examples

• A tester has an urn in front of him, in which he can not look into it. In it are red and green balls. Time can be taken for testing from the urn only one ball.

• We want to investigate the influence of diet on the mental development of children in children's homes. For this, we compare two groups of children with regard to their performance in cognitive tests: one sample is nourished by the conventional plan, the other one can be a particularly healthy diet We suspect that the healthy diet has a positive effect on cognitive performance.

Note: For beta (and alpha) are conditional probabilities.