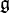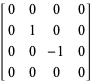Adjoint representation

In mathematics, the adjoint representations of Lie groups and Lie algebras play an important role in differential geometry, representation theory and mathematical physics.

Lie groups and Lie algebras

A Lie group is a differentiable manifold, which also has the structure of a group so that the group join and the inversion are infinitely differentiable.

The Lie algebra of a Lie group is the vector space of left - invariant vector fields with the commutator as Lie bracket. The Lie algebra can be identified in a canonical way with the tangent space at the neutral element of the Lie group:

Adjoint representations

Let be a Lie group with Lie algebra.

The conjugation with an element is represented by

Defined mapping.

The adjoint representation

Is defined by

For all defined Lie group homomorphism.

Is also referred to as the adjoint representation of the induced Lie algebra homomorphism

Because every finite- dimensional real Lie algebra up to isomorphism a unique simply connected Lie group are according to Lie's records with, you can define the adjoint representation for each such Lie algebra.

Explicit description

The adjoint representation of a Lie algebra corresponds to applying the Lie bracket: it is

For everyone.

For matrix groups, that is, closed subsets of, can also be the adjoint representation of the Lie group explicitly describe: according to the canonical identification of a subset of valid

For everyone.