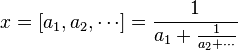Baire space (set theory)

The Baire space ( after the French mathematician René Louis Baire ) is a topological space. It is of particular importance for the descriptive set theory, as many sentences that can be proved for the Baire space directly transferred to general Polish spaces, such as on or the Hilbert cube. In evidence, it can be easier to handle than the real numbers. It is defined as the set of all sequences of natural numbers, quantities such consequences are considered to be open if they are the union of sets of sequences with a common prefix.

The topology of the Baire space

The topology of the Baire space can be defined as the countable product topology of the discrete topology on, which is equivalent to the above intuitive definition of open sets, the sets of sequences with a common prefix, thereby forming a basis for the topology. We show that the Baire space is actually a Polish space. Since the discrete topology is metrizable, and the countable product is metrizable, it can be specified in concrete terms, a simple metric:

And the first digit designates, in which the consequences and different. There even is an ultrametric. The Baire space is separable, since the set of all sequences that take the value zero at a certain position is countable and is dense in. The completeness can show analogously to the real numbers, since the Baire space permits nested intervals in a very natural way.

Importance for the descriptive set theory

Its universal application receives the Baire space in that each Polish space the image of a continuous map from the Baire space, which means that a continuous surjection from Polish into any room exists.

Properties of the topology

Each point in the Baire space, the set of all sets as a countable neighborhood base, in which case the set of all points in the Baire space call, so that the first digits with those of the same. This allows a natural characterization of the continuity of a function at a point: is continuous at the point when there is for each one, so that the first digits determined by the first digits of.

Also allows the convergence of a sequence of points of the Baire space characterize: A sequence converges if and only if there exists for each one, so always match the first digits from th follower. This distinguishes the Baire space of real numbers, where edge cases occur in which this property is violated ( The episode 0.9, 0.99, 0.999, ... converges to the one).

The Baire space is - like any ultrametrisierbare room - totally disconnected, every subspace with at least two elements can be divided into two disjoint open sets. For open sets you can see this very easily: you Represents an open set as a set of prefixes, which is always possible, since the amounts of sequences with a specific prefix form a basis, so can the open set on by " attach " additional characters a prefix into disjoint open subsets divide. An example: The set of all starting with zero consequences in Baire space is open, it can be in the open set of sequences starting with zero, followed by an even number and the open set of sequences starting with zero, followed by an odd number divide. The property transfers for non- open sets on the subspace topology.

In the Baire space there are no isolated points, that is, it is a perfect Polish space.

The Baire space can also be in the real numbers Embed: By means of the continued fraction expansion can be shown that it is homeomorphic to the subspace of irrational numbers. The function

Is a homeomorphism onto its image, as it is precisely the set of irrational numbers greater. This in turn is connected by means of the homeomorphism homeomorphic to the irrational numbers in the interval. Thus, the irrational numbers countable topological sum of the Baire space homeomorphic quantities and thus also homeomorphic to the Baire space. Note that this part of space of the real numbers is not completed and therefore, the conventional inherited of real numbers metric is not fully on it.

For universality

As already noted is a fundamental property of Baire space, that every Polish space is the continuous image of the Baire space. So be a Polish space. Now can be constructed for all finite words open subsets with the following properties:

• For.

For this you need the separability: For each there exists a countable dense subset sufficiently small open balls to then satisfy the desired properties. Now define with you, with the prefix of the length of call. Due to the completeness of the space is uniquely defined by the Intervallschachtelungsprinzip. is continuous, since it receives Convergence: points of Baire space with a common prefix are mapped to points in, so that the image sequence of a convergent sequence converges to the image of the limit. There even exists a continuous bijection from a closed subspace by (note that this need not be a homeomorphism, but the topology can coarsen also - the category of Polish spaces is not balanced - especially such a subspace is totally disconnected, so he is not about can be homeomorphic to the reals ). For this purpose, we choose instead of open sets - sets that are disjoint in addition in addition to the above conditions at any level in pairs, ie for. Such is obtained approximately by. Restricts you now address the items, so just the same for the non-empty and, to obtain the desired continuous bijection.

Retrakte

In the Baire space every closed subspace is (these are especially Polish) a retract. The proof is on the ceiling subspace as before with open sets with the additional condition that for all. The above figure is constructed in turn steadily and each element of is a fixed point. Thus it is a retraction and the subspace a retract. Restriction provides, that every closed subspace of a closed subspace is a retract of the latter. Conversely, it must, as in any Hausdorff space every retract to be completed, that is, the Retrakte are hereby fully characterized.