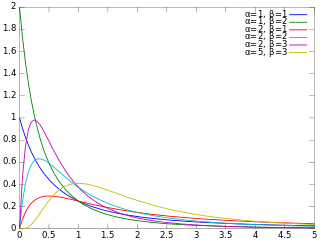
Beta prime distribution

(Also known as beta or inverse primary distribution beta distribution ) the beta prime distribution Bp is a univariate distribution for continuous random variables, with two parameters α and β. It is a special case of the gamma-gamma distribution and thus a mixed distribution.

The density function is:

Here B ( α, β ) the Beta function.

With expected value

Mode

And variance

Relationship to the gamma distribution

If the second parameter ε of the gamma distribution G (a, ε ) is a random variable that is distributed as a gamma distribution G (b, 1), then the company resulting random variable as a beta primary distribution Bp (a, b ) distributed.

Relation to the gamma distribution gamma

A gamma - gamma distribution Gg (a, b = 1, d ) corresponds to a beta primary distribution Bp ( α = d, β = a)

Discrete univariate distributions for finite sets: Benford | Bernoulli | beta - binomial | binomial | categorical | hypergeometric | Rademacher | generalized binomial | Zipf | Zipf - Mandelbrot

Discrete univariate distributions for infinite sets: Boltzmann | Conway - Maxwell - Poisson | negative binomial | extended negative binomial | Compound Poisson | discrete uniform | discrete phase -type | Gauss - Kuzmin | geometric | logarithmic | parabolic fractal | Poisson | Poisson - Gamma | Skellam | Yule- Simon | Zeta

Continuous univariate distributions with compact interval: Beta | Cantor | Kumaraswamy | raised cosine | Triangle | U - square | steady uniform | Wigner semicircle

Continuous univariate distributions with half-open interval: Beta prime | Bose -Einstein | Burr | Chi-Square | Coxian | Erlang | Exponential | F | Fermi -Dirac | Folded normal | Fréchet | Gamma | Gamma Gamma | extreme | generalized inverse Gaussian | semi logistically | semi- normal | Hotelling's T-square | hyper- exponential | hypoexponential | inverse chi-square | scale - inverse- chi-square | inverse Normal | inverse gamma | Levy | log-normal | log- logistically | Maxwell -Boltzmann | Maxwell speed | Nakagami | not centered chi-square | Pareto | Phase -Type | Rayleigh | relativistic Breit-Wigner | Rice | Rosin -Rammler | shifted Gompertz | truncated normal | Type -2 Gumbel | Weibull | Wilks ' lambda

Continuous univariate distributions with unbounded interval: Cauchy | extreme | exponentially Power | Fishers z | Fisher - Tippett ( Gumbel ) | generalized hyperbolic | Hyperbolic- secant | Landau | Laplace | alpha- stable | logistics | normal ( Gaussian ) | normal - inverse Gauß'sch | skew - normal | Student's t | Type -1 Gumbel | Variance gamma | Voigt

Discrete multivariate distributions: Ewen | multinomial | Dirichlet compound multinomial

Continuous multivariate distributions: Dirichlet | generalized Dirichlet | multivariate normal | multivariate Student | normal scaled inverse gamma | Normal - Gamma

Multivariate matrix distributions: Inverse Wishart | matrix normal | Wishart

• Probability distribution