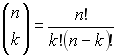Binomial coefficient

The binomial coefficient is a mathematical function, which can be solved one of the fundamental tasks of combinatorics. It specifies on how many different types you can select objects from a set of different objects ( without replacement, without regard to the order). The binomial coefficient is therefore the number of subsets of a - element set.

" 49 6 " (or " 45 6 " in Austria and Switzerland ), for example, the number of possible contractions in the lottery (excluding the bonus number ).

A binomial coefficient depends on two numbers and down. He is the symbol

Written and spoken as "n over k ", " k of n " or "n low k". The abbreviation for nCr from n choose r is given as a label on pocket calculators.

The name given these numbers, as they occur as coefficients in the powers of the binomial; whichever is the so-called binomial theorem:

An extension of that coming from the combinatorics binomial coefficient represents the general binomial coefficient, which is used in the analysis.

5.1 Example
5.2 Combinatorial proofs

6.1 sums with binomial coefficients
6.2 sums with alternating binomial coefficients
6.3 sum of shifted binomial coefficients
6.4 Vandermonde identity

7.1 generalization
7.2 Binomial series
7.3 sum expression for the beta function
7.4 Gaussian product representation for the gamma function
7.5 Digammafunktion and Euler - Mascheroni constant

Definition

Of a complex number and a non-negative integer the binomial coefficient "n over k " is defined as follows:

The Faculty of designated. The empty product () is.

If it is in a non-negative integer, we can use the well-known from the combinatorial definition:

Properties

If besides also restricted to non-negative integers, then:

Is always a non-negative integer.
Is it so applies

( for the right summand ).

In the general case, real or complex values for some of the expressions set forth herein may be undefined in the above sense, that is, if should no longer be entirely non-negative; which relates to the statements, and. It appears, however, that these statements are correct if you allow according to the below analytical generalization of the beta function for complex values .

Symmetry of the binomial coefficients

Integer binomial coefficients are symmetric in the sense of

For all non-negative and.

Recursive representation and Pascal 's Triangle

For the binomial coefficients of non-negative integers and one has the following recursive representation:

This formula can also be used to determine all the binomial coefficients up to a predetermined limit for a scheme to is Pascal's Triangle: where it meets the design specification that each number is the sum of two standing on their numbers (in the formula above by replace ):

Or the other way around ( by replacing ):

Proof:

The coefficients can be found here in the -th row of the - th position (both from zero counting! )

The same triangle shown in the Binomialsymbolen:

Algorithm for efficient calculation

For integer, an efficient algorithm which product formula exists

The binomial coefficient applies. Due to the constant change between multiplication and division, the intermediate results do not grow on unnecessarily. In addition, all intermediate results are natural numbers.

To avoid unnecessary computational cost, is calculated in the case of the binomial coefficients:

The following pseudo code illustrates the calculation of:

Binomial coefficient ( n, k) 1 if k = 0 then Return 1 2 if 2k > n 3 then do the results from binomial coefficient (n, nk ) 4 otherwise result from lead n -k 1 5 of i from 2 to k 6 leads from earnings earnings ( n - k i) 7 result result: i 8 Attributable profit The calculation method also use calculators if they offer the feature. Otherwise, the computational capacity of n = 69 would be exhausted. The labeling of the function key with nCr describes the sequence of input values in infix notation; first n number of elements, then the function key combinations, then the number of selected objects r ( in the article abbreviated k).

The calculation nPr (English permutation ) takes into account the permutations of r elements, the division by r! omitted:

The binomial coefficient in combinatorics

The combinatorial definition of a number of subsets of a - element set plays a central role in enumerative combinatorics.

It can be clearly interpreted like this: First, you count all tuples with pairwise different elements that can be put together from the -element output quantity. There are ways of choosing the first tuple element. After any election of this first, there are only choices for the second element, at its option, only for the third, etc., to candidates for the -th and last tuple element. The total number of such tuples is compiled so the digit product, with the help of the faculty as can be noted. Now, however, the counted -tuple permutations are exactly each other and thus corresponds to einundderselben -element subset. After division by this counting multiplicities thus results in fact than the required number of groups.

Another, more symmetrical illustration emphasizes not and elements of the act of selecting of elements, but the aspect of the decomposition into two subsets. Suppose a -element Ausgangstupel consists of red and white somehow strung elements. By forming all permutations of this alignment, as are each of them indistinguishable in color, because the permutations of the red elements to each other do not change the color sequence, just as each of them independent permutations within the white. So there are only different color sequences of length with all possible different assignments by each red elements. Each sequence can now be unambiguously but one of the subsets of a - element set to assign. The same is true because of the symmetry of red and white or and also for the complementary subsets. The total number of the subsets is therefore ever.

The set of all subsets of a set is sometimes referred to because of their thickness with. This is true for any finite set:

Example

The number of possible contractions or lottery tickets at the German Lotto 6 from 49 (without bonus number or super number)

Obviously there is only one chance to hit 6. one of the possibilities for 0 right thing, namely, to select all 6 Tips from the 43 wrong. The number of different tips with 5 correct results very easy to 6 ⋅ 43 = 258, because there are 6 ways to tap only 5 of the 6 numbers drawn (or omit it), and then 43 each = 49 - 6 options, the to put boisterous Tip on one of the 43 wrong numbers. In general, the number of different tips with r correct results in 6 out of 49 for the same consideration. At 6, 0 and 5 Right hardly noticeable that the factors used, and really simple binomial coefficients. The sum of all numbers called Tip yields of course the total number 13983816 all possible tips - this follows from the Vandermonde 's identity given below.

The probability of 6 scored with a tip right is therefore 1/13983816 which is for 5 correct 258/13983816. 0 for right result with 6096454/13983816 already about 44%. The overall probability for r right is a special case of the hypergeometric distribution, which combines just three binomial coefficients such.

Combinatorial proofs

The combinatorial interpretation also allows simple proofs of relations between binomial coefficients, such as double counting. Example: For the following applies:

Proof: Let a - element set and a fixed element. Then decompose the subsets of two classes:

The subsets that include; So they are made together with an -element subset of the - element set,
The subsets that are not included; they are - element subsets of the - element set.

Expressions with binomial coefficients

Sums with binomial coefficients

This formula is a combinatorial facts as a basis. Since the number of all subsets of an amount corresponding with elements given by the summation of the number of all its subsets, ie. The formula can be derived also from the binomial theorem by setting.

Sums with alternating binomial coefficients

This formula follows from the odd symmetry of the binomial coefficients. For arbitrary they can be derived from the binomial theorem, by and (or and ) is set.

Sum of shifted binomial coefficients

Vandermonde identity

There is also a combinatorial argument: The right side corresponds to the number of subsets of a - element set of balls. One can now imagine that the balls have two different colors: balls are red and green balls. A - element subset is then composed of a certain number of red balls and lots of green. For each possible are the corresponding term on the left side of the number of possibilities for such a split between red and green balls. The sum gives the total number. An often perceived as a simple proof uses the binomial theorem in the form

And approach

And comparing coefficients.

In the special case follows from the Vandermonde 's identity following formula for the sums of squares

Binomial coefficients in the Analysis

Generalization

A generalization, which plays a role in the analysis, obtained when one allows for an arbitrary complex number, but still requires as an integer. In this case,

The binomial coefficient " on" ( in the case of the blank the product is defined as 1). This definition is for non-negative integer with the combinatorial definition (ie the definition of as the number of all subsets of a fixed - element set ), respectively, and for non-negative with the algebraic definition (ie the definition of as the product ).

For example, is

And

The second parameter can be generalized to arbitrary complex assignment when defined using the beta function for:

Where the gamma function called. Is it or is a negative integer, then the value of the right-hand side is 0, because the non- positive integers, the ( single ) pole are.

Obviously still applies the symmetry relationship

In particular:

Whole and in nichtnegativem

To extract the sign of the first parameter, provided that it is an integer, the relation can be

Specify.

In general, for complex, the relationship

Another generalization offer the multinomial, which are required in the generalization of the binomial to multinomial theorem.

Binomial series

For and with one obtains the relationship

Which is a generalization of the geometric series and is one of the binomial series.

Is, as well as the following series converges according to

( For more precise conditions and see Article binomial series. )

Sum expression for the beta function

Another relationship can be relatively easy for all prove by induction,

Resulting directly the symmetry

Followed. A generalization for with and is

Gaussian product representation for the gamma function

With the latest formula from the previous section is

Considering the case that breaks replaced in the sum by integrals according to

And summarizes the sum of the powers of the binomial corresponding together, one obtains

Where the last integral the substitution was applied. Finally, one has the equation

Resulting in through the border crossing directly the Gaussian product representation of the gamma function,

Results.

Digammafunktion and Euler - Mascheroni constant

For with

Which can also be proved via induction on. For the special case of this equation simplifies to

The sequence of harmonic numbers, so the partial sums of the harmonic series. The transformation of the left-hand sum in a row ( instead of limit ) is allowed due to

On the other hand represented as

With the Digammafunktion and the Euler - Mascheroni constant

Can on complex values - to be continued - except on the negative integers. One gets then the series

As complex interpolation of the result of the harmonic numbers.