Branch-and-Bound

Branch -and-bound (branch and bound ) is a mathematical method commonly used in Operations Research, whose goal is to find a best solution for a given integer optimization problem. Branch -and-bound leads to a decision tree, but it itself is not a specific method, but a method of treatment, a meta - method. For concrete combinatorial optimization problems arise accordingly adapted branch-and- bound algorithms.

• 2.1 Solution
• 2.2 A simple example
• 2.3 Assessment of the method

The principle

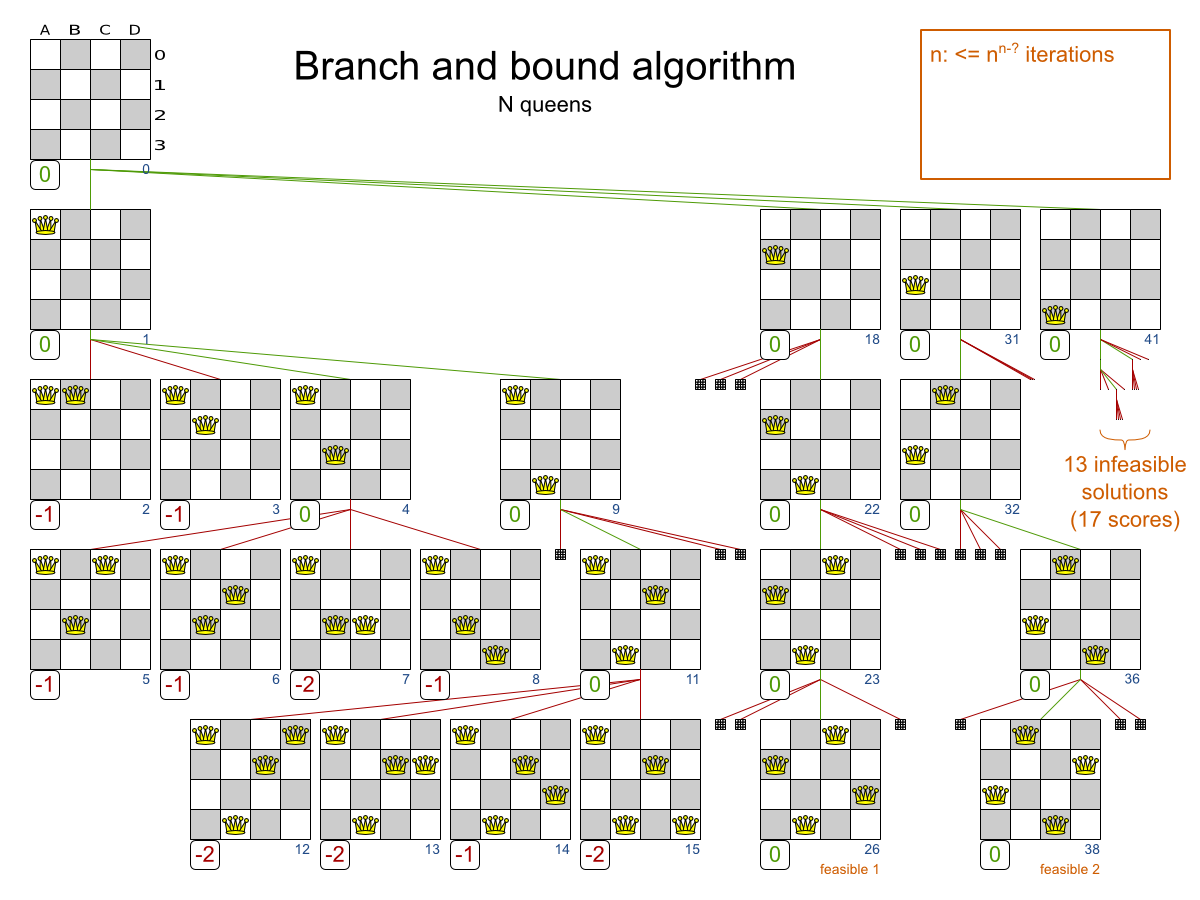
In the optimization problem in the allowable range is a discrete set, possibly even last. Durchzuprobieren All approved assignments, usually fails due to unacceptably long computation times. Therefore, it is gradually split into a plurality of subsets ( Branch). Using appropriate barriers ( Bound ) to many sub-optimal assignments are identified and separated out, so that the solution to durchmusternde space is kept small. In the worst case, all assignments are listed ( complete enumeration).

Branch, the branch

Said dividing step (Branch step) is used to split the problem present in two or more sub-problems, representing a simplification of the original problem. By recursively performing the division step for the obtained subproblems results in a tree structure. There are various competitions for the selection of the next node to be processed in the layout tree, which have different objectives. The following are two methods commonly used are described below:

Depth-first search: Of the unprocessed subproblems is chosen the one that was inserted last ( Last In - First Out). With this selection rule, the method operates in the tree as quickly as possible into the depths, so that in general, very quickly a feasible solution is obtained, but on their quality anything can be said.

Breadth-first search: Of the unprocessed subproblems is chosen the one which was inserted first into the tree (First In - First Out). Using this selection rule, the nodes are processed in the tree per level before deeper nodes are considered. An acceptable solution is obtained relatively late in the rule, but tends to have a good solution value. This strategy also tends to be early to useful lower bounds.

The method can be combined. A first solution can be determined, for example, a depth first search, and then already to have a global upper or lower bound in a subsequent breadth-first search.

The Bound - step has, that is, in subsequent calculations no longer be considered the task of " cutting off " certain branches of the tree, so as to limit the computational effort. This is achieved by calculating the algorithm, and comparing the upper and lower bound:

• Upper bounds ( upper bound ) arising out of any feasible solution. But may optionally be previously used heuristics.
• In order to find good lower bounds ( lower bound ), is often placed a relaxation based. This is a defined on a set, easy function to be calculated with for all. The relaxed problem is easily solvable in and possess an optimal solution. Then obvious to all. When is the optimal solution of the non- relaxed problem.

These considerations are also applicable to sub-problems, ie where the amount has already been split. You already know a feasible solution and the lower bound for a subproblem is greater than, then one does not need to examine that part of the problem further because it does not provide an optimal solution.

Dominance

From dominance occurs when, for each assignment of a subset of a non- inferior feasible solution can be constructed. If not all optimal solutions sought, but only one, then the search is unnecessary in, even if the barriers alone are not sufficient to exclude from further screening. This increases the efficiency of the process sometimes considerably, for example in multi-dimensional cutting problem, although dominance tests do not belong to the original method of branch- and-bound.

Example: for must be resolved. A lower bound follows at once by all summands are estimated downward, ie. Branch-and - Bound apply without dominance considerations, turns out to be unnecessarily burdensome. Because is as small as possible to choose, no matter how large, that is. For is; at is, and thus not optimal. The only solution is optimal.

Application to problems of integer linear optimization

The general integer linear programming problem has the form

• Maximize
• Subject to the constraint and
• With A: M × N matrix
• X: n -dimensional vector
• A: n- dimensional vector
• B: m -dimensional vector
• A · x: scalar product, linear function with n variables, real value
• Ax: m-dimensional vector x is formed as a matrix-vector product of the matrix A and the n-dimensional vector.

With neglect of the continuous relaxation integrality is obtained which can be solved by the simplex method. Due to the required integrality of the initial problem but does not belong to the linear optimization problems.

Solution

The problem can be solved using the branch- and-bound method. First set than previously best objective function value and omitted the Ganzzahligkeitsbedingung:

• Maximize
• Subject to the constraints and.

The resulting problem is called P0. This now -linear optimization problem to solve with the simplex method. Generally, the solution will not be an integer, i.e., not continuous integral. Without loss of generality, this would also apply.

Now try to find solutions with integer. Be the greatest integer less than. Then we formulated two new linear optimization problems and such that the solution previously found is excluded in each case:

• - Maximize
• Subject to the constraints

• - Maximize
• Subject to the constraints

Such a division into sub- problems called branch (English branch ).

Both subproblems are solved with the dual simplex method. The following cases can occur:

In case ( 1), the subproblem done. In other cases, the same is true if and only an optimal solution is sought or is and all optimal solutions are sought. Otherwise is memorized in the case (2) through the solution found as best ever replaced, while in the case (3) the sub-problem is further split.

In this way, the entire solution space is searched and an optimal solution is found, if there is one and the process was not terminated prematurely. It is quite possible that despite exhaustive search finds no solution. Then the original problem has no feasible solutions.

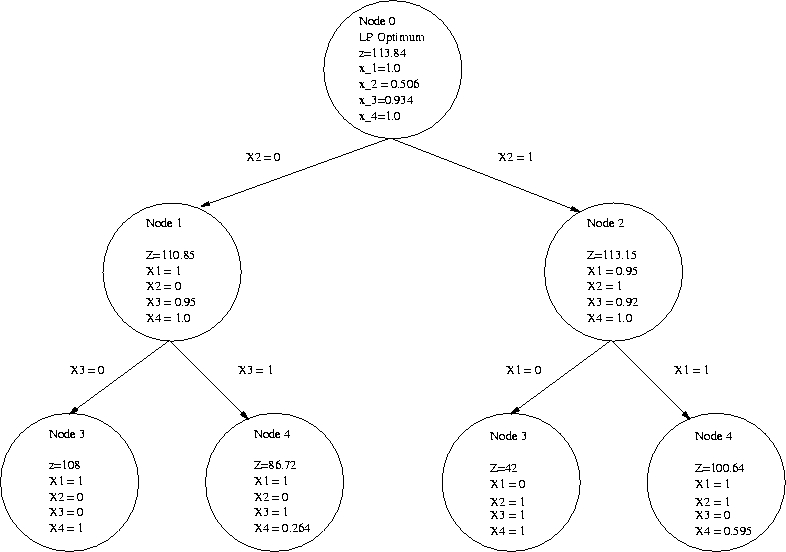
A simple example

Based on a concrete task, we show the method.

The initial problem is:

• Maximize
• With the constraints   integer

We omit the Ganzzahligkeitsbedingung and find the simplex method, the optimal solution

We will continue with the aim to find a solution with integer. We make two further optimization tasks, one with the additional constraint, the other with.

• - Maximize
• With the constraints

• - Maximize
• With the constraints

The problem has the solution

Since and are integers, this is a feasible solution of the original problem. We do not yet know if there is a better solution.

We solve the problem and get:

Again, this is a feasible solution for the integer. Since both for and for the objective function takes the value, the problem has two optimal solutions.

Assessment of the procedure

In the branch-and- bound algorithm more - must be stored optimization problems, managed and solved using the simplex method - many in unfavorable cases. In particular, for large problems which can have hundreds of thousands of variables and constraints, this leads to a high computational and memory requirements. But one avoids the disadvantage of the cutting-plane method Gomory, complicate the search for a solution in which numerical problems due to lack of precision of the number representation in the computer. In practice, both methods for branch-and -cut are combined in solving integer programming problems often. In this case, the root node and sometimes separated in other nodes of the branch- and-bound tree cutting planes to tighten the linear relaxation.

History

The idea of Branch-and - Bound was first formulated in 1960 by AH country and AG Doig in the field of Operations Research. RJ Dakin gave in 1965 to a simple -to-implement algorithm.