Capital Asset Pricing Model

The Capital Asset Pricing Model (CAPM; into German: pricing model for capital goods or Kapitalgutpreismodell ) is a capital market equilibrium model that extends the portfolio theory to the question of which part of the overall risk of an investment property is not by spreading the risk ( diversification) must be eliminated and explains how risky investment opportunities are valued in the capital market. The core of the CAPM, the model of the securities line describes a linear dependence of the expected returns of an investment of only a risk determinant ( one-factor model). The aim of the CAPM is ultimately equilibrium rates for individual risky investment opportunities ('the securities) to derive the portfolio context under uncertainty ( risk).

It is especially used for the determination of risk-adjusted discount rates ( cost of capital) used in the business valuation (see the evaluation standard of the Institute of German Auditors, IDW S1). However, empirical studies doubt the suitability of the CAPMs to predict the expected return of stocks and (eg a company to be valued ) adequately capture the valuation-relevant risk of the property being valued (see section on empirical testing ).

History

The CAPM was developed independently by William F. Sharpe, John Lintner and Jan Mossin in the 1960s and is based on the portfolio theory by Harry Markowitz.

Problem

Subject of portfolio theory is the investment decision of a (mostly ) risk-averse investor for selection of risky and risk-free securities. Under the assumption of normal distribution for asset returns, this decision depends solely on the expected risk and return of the securities. The expected return from the mean, the risk from the standard deviation of past price data is derived. The basic idea of portfolio theory Markowitz is the possibility of diversification through the formation of securities portfolios.

The CAPM goes a step further and determined theoretical equilibrium rates that adjust when risk-averse market participants put together according to the portfolio theory, efficient portfolios.

The pricing of a security has an impact on the pricing of other securities. The equilibrium prices have to be determined simultaneously.

Equilibrium prices are important for aggregate risk premium or risk reductions:

• In the business valuation they are used to determine the cost of capital ( WACC).
• With the equilibrium prices can assess the performance of equity funds. This makes it possible to make a statement whether the additional risk is appropriate based on the average extra return.

Composition of the model

The precursor of the CAPM is the model of the capital market line (KML, Eng. Capital Market Line CML), whereas the model of the securities market line (WML, Eng. Security Market Line, SML ) forms the actual core model. The CAPM is based on the same conditions as on the portfolio theory. There are also the simplistic assumptions of perfect capital markets, risk aversion and homogeneous investor expectations, and normally distributed asset returns.

From these assumptions it follows that all investors hold a compound in the same way in the portfolio market equilibrium, if risky securities and a risk-free investment ( capital market ) are available. More specifically, each investor holds a mixture of the market portfolio M and the risk-free investment. In this so-called market portfolio includes all traded risk- haftenen securities in proportion to their market values ​​are available. The assumption of steady state means that if there would not be efficient securities, they would be sold and exchanged for efficient securities. The sale of such securities pushes their price (if the Competitivity condition will not be accepted), so does the yield of the security concerned rise. In equilibrium, all such transactions have been completed, which means that there are no more securities on the capital market under consideration that are not efficient. Therefore, the market portfolio consists only of efficient securities and therefore must itself be efficient.

Are the expected returns and risks of the individual securities known, can also be the expected return and the risk of the market portfolio calculated. The expected return on the market portfolio is referred to in the capital market theory as a " cost of capital under risk " or " risk-adjusted cost of capital".

The possibility of unlimited risk to invest money or take, the investor desired risk position, in a next step, depending on its degree of risk aversion by mixing the risk-free investment opportunity with an investment in the risk-efficient market portfolio (or at lower risk aversion by borrowing and investment in the produce market portfolio). This allocation of capital to be applied in a structured market portfolio is always identical regardless of personal risk appetite is called the Tobin separation or "Two Fund Separation".

To the expected return and the price of an individual security in the portfolio context derive in this model world on mathematical and statistical means, the following determinations are made:

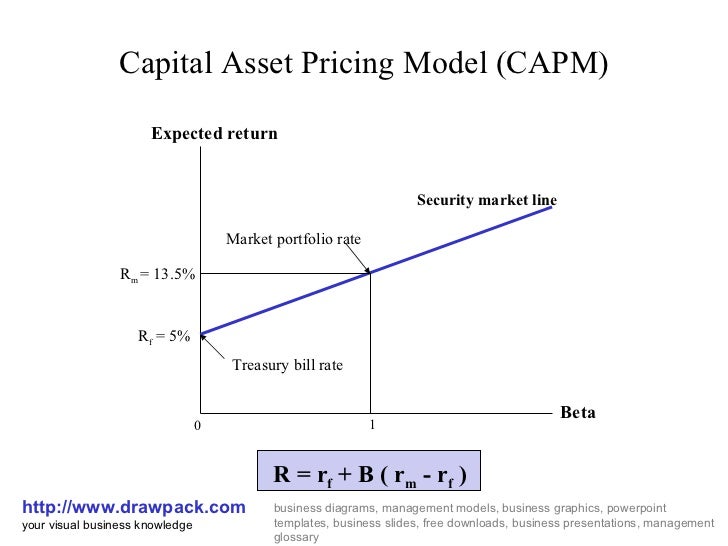
The difference between the expected return on the market portfolio M ( " cost of capital under uncertainty " ) and the safe interest rate is called market risk premium (MRO ). The risk amount of each security in a well- diversified portfolio is called beta ( β ). The risk of the market portfolio M itself is 1, the β - factor of an individual security is defined as the ratio of the statistical covariance of the security in the market portfolio M and the variance of the market portfolio. The beta factor refers only to the irreducible risk in the portfolio context ( the so-called " systematic risk " ) and thus represents the major contribution to risk of each portfolio

After a subsequent mathematical optimum determination is now as the central message of the CAPM:

With

The beta value for the safe installation Is the beta value for the market portfolio

Formula for calculating the risk-free rate from the other (known) parameters:

The expected return on a risky security ( eg shares ) shall be in the market equilibrium composed of the risk-free rate and a risk premium. The risk premium is the product of the market price of risk and the risk amount of the actual investment opportunity.

The following applies: The higher the beta of a security, the higher and vice versa its expected return. In other words, investors are only willing to hold a security with a high risk ( β ) when a correspondingly high rate of return can be expected.

Under the assumptions made einperiodiger planning can be converted easily into an equilibrium price for each security the determined rate of return. The equilibrium rate serves as a measure of whether a single security (portfolio ) is assessed in accordance with its risk by the market.

An alternative formulation of this equation yields the CAPM is the following " λ - notation "

With

In this formulation, the beta factor is split. It is clear that the expected return is dependent according to CAPM by the " market price of risk, the so-called Sharpe ratio ( a performance measure ). This is just the ratio of the market risk premium (MRI ) of the extent of market risk, which is the excess return per unit of risk. In size λ, the risk-return profile of alternative investments available on the market expresses. The degree of risk for the measured property ( uncertain return on the risky security) is expressed by? I, the standard deviation of these returns. The product x? I ρi, m expresses the degree of risk that the evaluation subject has to wear ( taking into account the risk diversification opportunities ).

In addition to the well-known " return equation " of the CAPM (see above) there is a consistent this " certainty equivalent variant". The value of a risky payment depending on the risks of this payment, expressed by their standard deviation as a risk measure is determined from the same assumption system immediately determined.

As a security equivalent variant, this equation is called because starting from the expected value of the payment risk reduction is performed and this result can be interpreted as the certainty equivalent of the uncertain payment and without reference to a utility function (see expected utility theory ) is derived. Inherent is the assumption that economic agents of the values ​​with respect to the expected value and the standard deviation of the considered uncertain payment ( μ, σ ) principle. The main advantage of this in practice less common variant of the CAPM is that an assessment of uncertain cash flows of the property being valued is possible without recourse to the capital market data, which are used in the application of the CAPM in valuation practice to determine the above-defined beta factor. Instead of risk information on the price development of the risky security ( eg a share) are directly risk information about the actual evaluation object (eg a company ), so used via the so-called " income risks " (volatility of payment).

It can be shown that the above equation also without many of the restrictive assumptions of the CAPM (such as market equilibrium ) with the method of " imperfect replication " can be derived. In these methods, the " imperfect replication " for matching of valuation equations is based on the following assumption: two uncertain payments ( at the same time ) have the same value if they are in the expected value and the selected risk measure - match - in the CAPM ie the standard deviation.

Applications

• Stock Valuation
• Performance Analysis
• Evaluation of investment projects, company valuation
• Portfolio Management
• Market value -maximizing investment decision

Critical appraisal of the CAPM

The strict assumptions of the CAPM may seem unrealistic at first glance. However, many of the assumptions can be relaxed ( relaxed ), without compromising the basic statements of CAPMs in question. In particular, in the 1970s and 80s, some of the original model assumptions have been replaced by more realistic. This shows that even under less stringent assumptions, the core message of the model of the securities line still valid. Various observations (anomalies ) are documented in numerous empirical studies that are not compatible with the CAPM. These include the value effect, the small company effect Momentumeffekt and the January effect. See also the Fama - French three- factor model. However, Sharpe already expressed in 1964, that a theory should not be checked in the realism of their assumptions, but the acceptability of its implications. Thus, the CAPM provides not only the best-known explanation for the exchange relationship ( trade-off ) between risk and return, but, for example, an important tool in measuring the performance of investment funds.

Especially in the valuation of unquoted companies limitations of the applicability of the Capital Asset Pricing Model (CAPM ) are considered in the determination of cost of capital ( or risk reductions ).

One empirical testing the CAPM deprivation because the market portfolio of all risky assets will not let reconstruct criticized Roll. Because of this, we draw on sub-portfolios. Tests of these sub-portfolios give only information about the risk efficiency of these sub-portfolios. Moreover, the CAPM can the claim to explain the stock market, in reality, not be fair, since hardly a state of equilibrium can postulate for real capital markets.

The problem for the empirical test of the CAPM is, furthermore, that it is sometimes used as a prediction model. Tests on the efficiency of a risk portfolios are, however, performed only on the basis of actual market prices from the past and usually do not consider the expectations of investors. Further problems in the empirical verification are the individual behavior of investors, their impact on the stock market, structural changes of the portfolio and data gaps. Actually not at all examined values ​​and time periods, data are available, allowing for missing data, certain assumptions must be made.

Empirical studies of the CAPM show in the great majority " unexpected ", ie can not be explained by beta influences on stock returns, so-called " anomalies ". Thus, the investigation proved by Banz (1981), the firm size effect ( " size effect"). The study by Basu (1977 ) finds that stocks with low valuations (PER ) can expect an above-average high, can not be explained by the CAPM beta returns.

Starting developed from an empirical study in 1992 Eugene Fama and Kenneth French in 1993, the three-factor model as a forecast stronger alternative to the CAPM. It refers to both the price- to-book ratio ( "Value " factor ") and company size ( market value ) as explanatory factors for the stock returns one. These results are confirmed for the German stock market. Carharts (1997) derived therefrom four-factor model takes into account the facts revealed in many empirical studies Momentum factor as a further explanation of the size of the stock return. Jegadeesh and Titman (1993 and 2011 ) show again a strong ( risk-adjusted ) outperformance of momentum investment strategies. Stocks with the highest return over the last three to twelve months draw a significantly above-average returns over the next three to six months.

Walk Häusl (2012 ) shows the existence of a significant negative risk-return relationship for the stock market and thus represents a key implication of the CAPM in question: more risk leads to a higher expected return. It even shows that stocks with lower volatility also a very low beta and at the same time a very clear positive alpha exhibit, while the poor yield stocks with high volatility a beta greater than one and have negative alpha.

Furthermore, a Gaussian normal distribution of returns is assumed for the CAPM implicitly. In the capital markets, however, fluctuations in return were more recently with scattering using a multiple scattering ( " fat tails " ) are observed. This observation of the return distribution is, however, in a clear contradiction with the assumptions of the CAPM.

Ballwieser sees the CAPM as "all other" confirmed empirically and points to a corresponding statement of Kruschwitz, p 227: " In light of the numerous and quite contradictory tests well, the conclusion must be drawn that the CAPM today only small empirical finds support. The presentation has further shown that up to now no, true test 'of the CAPM is still unknown. "