Conditional entropy

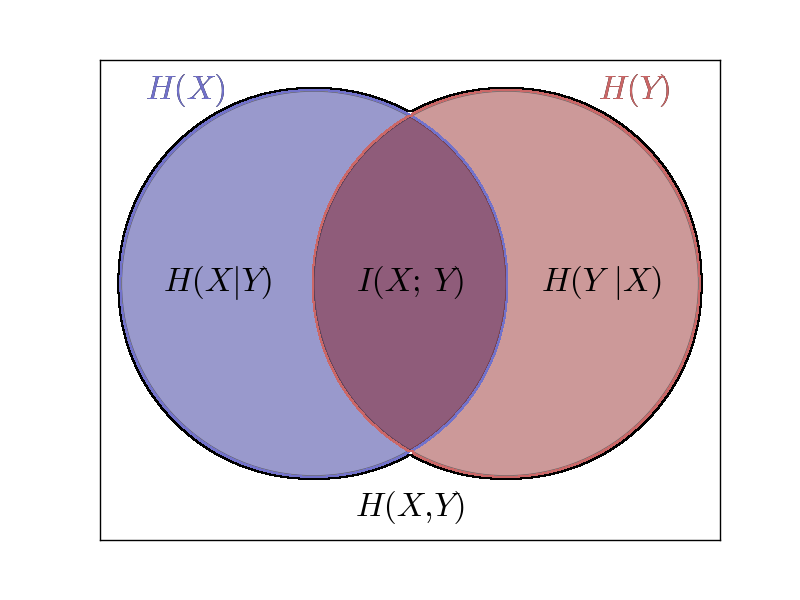
In information theory, the conditional entropy is a measure of the " uncertainty" about the value of a random variable, which remains after the result of another random variable is known. The conditional entropy is written and has a value between 0 and the initial entropy. It is measured in the same unit as the entropy.

Specifically, it has the value 0 if it can be determined from the value of functional, and the value if and stochastically independent.

Definition

Be a discrete random variable and its range of values ​​, ie is a countable set with. to accept with non-negative probability of each element. Then the entropy of by

, said (NAT ) can be assumed for the respective units for the values ​​2, typically (bit ), or e.

It is now with an event. Then one defines the conditional entropy of the probability by substituting given by the conditional probability that

Now be a discrete random variable with values ​​stock. Then the conditional entropy is defined by given as a weighted average of the conditional entropies of the events given for, ie

At a higher level of abstraction is at around the conditional expected value of the information function is given and at around the expected value of the function.

Properties

A simple calculation shows

So the uncertainty of given is equal to the uncertainty of the uncertainty and less of.

It is with equality if and only if and are stochastically independent. This follows from the fact that if and only if and are stochastically independent. It also means that, that is the complete received information is failure information. Analog is the complete information from the source X lost, so that no mutual information is then available.

Also, applies

With equality if and only if functional of dependent, ie. for a function

Blockentropie

Transferred to a multivariate random variable length, as a representation for a block of symbols, you can define the conditional entropy as the uncertainty of a symbol (after a certain predetermined block):

The Blockentropie called. For the conditional entropy, so the uncertainty of a symbol for a block follows:

The definitions of the Blockentropie and the conditional entropy are in the limit equivalent, cf Quellentropie.

Closely related to the conditional entropy is the mutual information, which indicates the strength of the statistical relationship between two random variables.

Example

Let X be a source periodically signs ... 00100010001000100010 ... sends.

Taking into account previous character now is the conditional entropy of the currently observable label shall be calculated.

No characters considered

The calculation is performed according to the definition of entropy.

Probability table:

A con sidered characters

Now let X: = x and Y: = xt -1. It results in the following probabilities:

Probability tables:

Where: P ( X | Y ) = P ( X = x | Y = y) = P ( xt = x | xt -1 = y)

Two characters considered

Let X: = x and Y: = (XT -2, xt -1). It results in the following probabilities:

Probability tables:

Where: P ( X | Y) = P ( xt | ( xt 2, xt -1))

Where: P (Y) = P ( yt, yt -1)

Three characters considered

Therefore the following characters have already been three consecutive characters known as is determined ( because the source behaves yes, periodically). Thus, one does not receive any new information on the next character. Thus, the entropy must be zero. This can also be seen from the probability table:

Where: P ( X | Y ) = P ( X = x | Y = y) = P (X = x | Y = ( xt -3, 2 xt, xt -1))

Impossible events are here marked with -, eg " " at y = ( 1,0,1 ). This edition is the given source never deliver, because follow a one always three zeros.

It is seen that in the table, no other probabilities occur as 0 or 1, since according to the definition of entropy applies H (0,1) = H ( 1,0 ) = 0, Finally, the entropy has H ( X | Y ) = be 0.

Explanation of the probability tables

The tables refer to the example above character sequence.

Where: P ( X | Y ) = P ( X = x | Y = y) = P (X = x | y = x -1) = p ( xt | xt -1)

Here's looking at you a sign X under the condition of the previous character Y. For example, if a character Y = 1, so the question is: How likely is the following character X = 0 or X = 1? For Y = 1, the next character X is always 0 Thus P ( X = 0 | Y = 1) = 1 from the fact that P (X = 1 | Y = 1) = 0 follows Moreover, since the row sum always is one.

Where: P (X) = P (X = ( xt, xt -1)) = P ( p ( xt ), p ( xt -1)) = p ( xt, xt -1)

Here one considers the frequency of occurrence of a combination of characters. One can read from the table that the letter combinations ( 0.1 ) and (1.0 ) occur as frequently. The sum of all matrix entries results in one.

Entropy and information content

The entropy is all the stronger in this example, are the more characters considered (see also: Markov process). If the number of characters taken into consideration is selected sufficiently large, so the entropy converges towards zero.

If you want the information content of the given string of n = calculate 12 characters, the result is, by definition, Itot = n ⋅ H ( X | Y) at ...