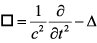D'Alembert operator

The d' Alembert operator ( after Jean Baptiste le Rond d' Alembert ) is a linear differential operator of second order, which is a generalization of the Laplace operator in four-dimensional Minkowski space. It is usually quoted as a square and, accordingly, as a square operator, Quabla (see nabla ) or (from the English coming ) referred to as Box Operator.

The d' Alembert operator is also called wave operator, because it is a central component of the wave equation as well as the more general Klein-Gordon equation.

Definition

Within the framework of special relativity theory (SRT ) is the Vierergradient, a covariant vector, by

Defined. The contravariant components arise by pulling up to the covariant index:

By combining the two operators, the lorentzinvariante d' Alembert operator can be formed:

It contains only second derivatives.

Sign conventions

As in the SRT, the sign of the signature of the metric depend usual. Often - as above - in SRT the convention ( , -, -, - ) is used for the signature of the Minkowski metric, otherwise one uses the convention ( -, , , ). For the first signature, the d' Alembert operator, as already shown above results to:

For other analogous signature results:

Both results are common. They differ only in sign. As a consequence, remains particularly noted that the wave equation (see below) does not depend on the convention chosen:

Wave equation

Originally, the d' Alembert operator comes from electrodynamics and results in the derivation of the wave equation. This is followed can be clearly seen that it is in the electrodynamics is a relativistic theory. In addition, the d' Alembert operator is a Lorentz scalar and therefore invariant under Lorentz transformations. He also plays thus an important role in relativistic electrodynamics. Using the d' Alembert operator can be written in a very compact form for a function, the wave equation

Green's function

A Green's function of the d' Alembert operator complies with the law of inverse as the defining equation

It denotes the Dirac delta distribution. Since this is a non- explicitly time - and space-dependent operator depends only on the differences as well, which is why we can put the primed coordinate zero without loss of generality. Of the Fourier transform

Then results in the following algebraic equation:

The poles are of exactly where the dispersion relation is satisfied for electromagnetic waves in vacuum (). The solutions of the homogeneous wave equation therefore coincide exactly with the poles of the Green's function, which is a typical response functions for resonance behavior.

In order to perform the inverse transformation, we consider the analytic continuation of complex frequencies. Using the residue calculus can be the poles to " circumvent ", where different paths correspond to different boundary conditions. We distinguish:

The Green's function in the frequency domain is to be understood in the limit, which corresponds to the different paths around the poles in the integral.

The factor corresponds to the propagation law of a spherical wave.

References and footnotes