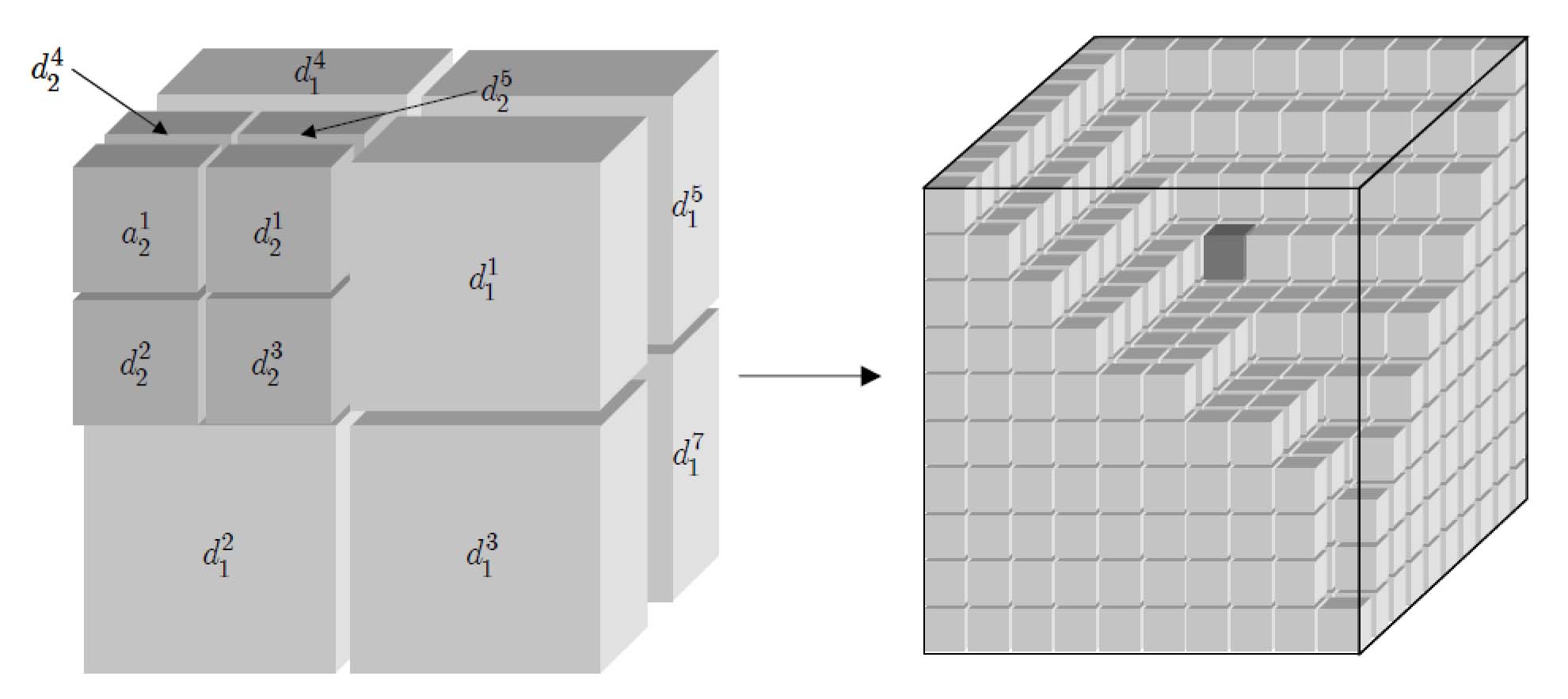
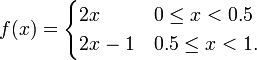Dyadic transformation

The Bernoulli map ( or Bernoulli shift) is a one-dimensional discrete-time dynamical system with piecewise - defined system function defined by the rule with the parameters.

For the Bernoulli figure provides interesting properties. This gives the iteration, ie for and for.

The Bernoulli map is chaotic.

With the start value one obtains the following iterates:

At this point, it is now evident why the Bernoulli map is also called a Bernoulli shift: the binary digit is shifted to the left, the decimal point will be truncated. That after each iteration, the system forgets exactly one digit of the binary representation ergo lost one bit of information.

In the binary representation, one sees more clearly that the Bernoulli figure has several invariant quantities in the parameter setting.

• All rational initial values ​​whose binary representation is finite, cause that the orbit after finitely many steps ends at the fixed point.
• All rational initial values ​​whose binary representation is periodic, mean that the orbit lands on a periodic attractor after finitely many steps.
• All irrational initial values ​​have an infinite and aperiodic binary representation and therefore form an aperiodic attractor.

• Nonlinear Dynamics