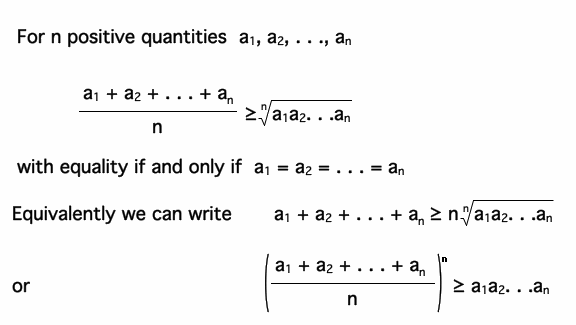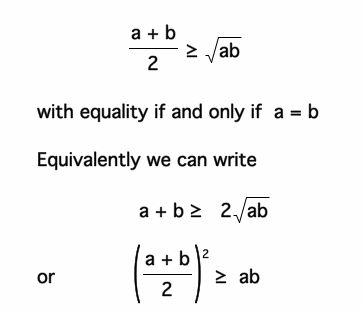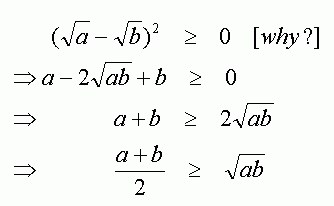Inequality of arithmetic and geometric means

Mathematics means the inequality of the arithmetic and geometric means that the arithmetic average is at least as large as the geometric mean. This inequality is one of the most important mathematical theorems. For it was known to Euclid; the first evidence for an arbitrary value of was published in 1729 by Colin Maclaurin

• 4.1 Inequality of the weighted arithmetic and geometric means
• 4.2 Inequality of the harmonic and geometric means
• 4.3 inequality of generalized means

Formal definition

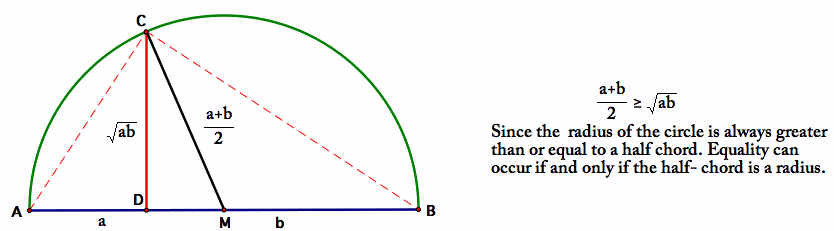
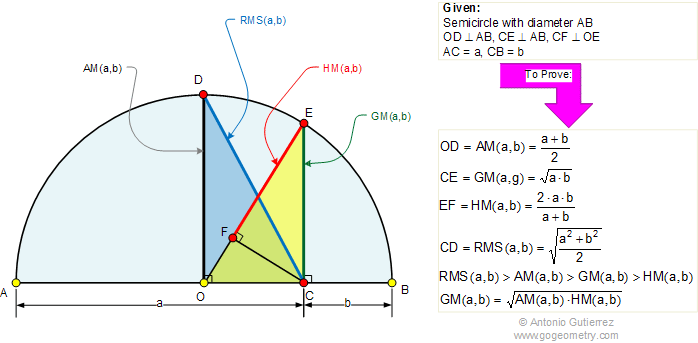
The inequality of the arithmetic and geometric mean is for non-negative numbers

The left-hand side of the inequality is the geometric mean and the arithmetic mean of the right side. It holds if equality if and only if.

Geometric interpretation

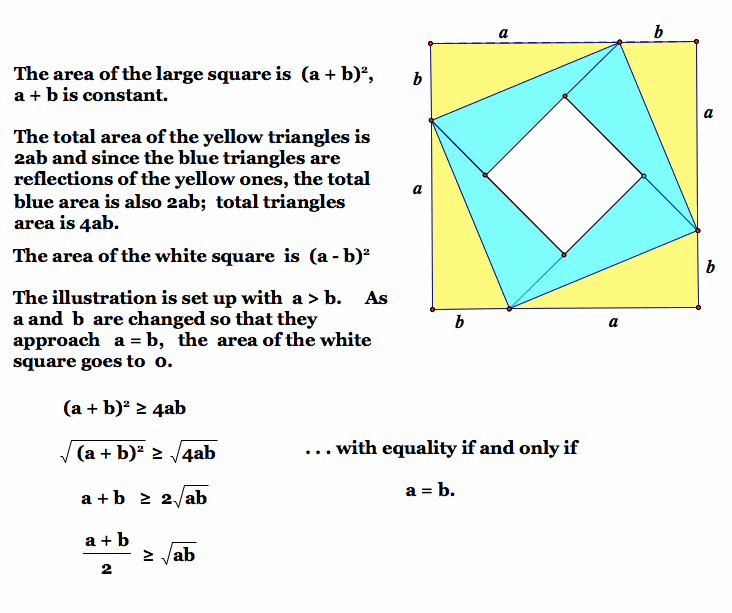
A rectangle with the sides and has the overall scope. A square having the same area is the circumference. For stating the inequality

So that among all rectangles with the same content of the circumference at least

Is, the square has this smallest scale.

In the event of the inequality indicates that, among all the blocks with the same volume of the cube edge length of the smallest total. The general inequality extends this idea to dimensions.

Evidence

For the case that a is equal to zero, the geometric mean is zero and the inequality is obviously met; can therefore be assumed in the following proofs.

Proof of the inequality between jens

The inequality of the arithmetic and geometric means can be, for example from jens between inequality prove: the logarithm function is concave, therefore, applies

Positive with.

By using the exponential function on both sides follows

For the results in exactly the inequality of the arithmetic and geometric means.

Proof of Polya

George Polya originates proves that only requires the relationship of the exponential function. For then applies

Multiplying these inequalities, we obtain

So

And thus

Inductive proofs

The proof of the inequality between jens and the Polya - proof are very easy to understand, but have the disadvantage that prior knowledge is required about the logarithm or the exponential function. For the investigation of the sequence used in the definition of exponential

But may be useful from the arithmetic and geometric mean the inequality. Methodologically, therefore, are often inductive evidence appropriately; these are for the inequality of the arithmetic and geometric means but relatively difficult.

Proof with forward-backward induction

An inductive proof of inequality of the arithmetic and geometric center is provided with " forward-backward induction " is possible. The forward step is carried out by proving the validity of 2n from the validity of the inequality for n. The backward step is carried out by the validity of the inequality for n, the validity for n- 1, by setting. This proof can be found already in Augustine Louis Cauchy.

Proof by Lemma

Another proof of the inequality of the arithmetic and geometric means follows from the lemma that for and it follows that. This evidence comes from G. Ehlers. The lemma can be proved for example by induction. Looking at the product and sets, so meet the defined so namely the condition of the lemma. It follows from the lemma

So

Inserting then provides the inequality of the arithmetic and geometric means.

Evidence from Bernoulli 's inequality

A direct inductive proof is possible with the help of Bernoulli's inequality: Let without loss of generality element of the maximum and the arithmetic mean of. Then, and follows from the Bernoulli's inequality that

Provides multiplication by

Where the last inequality holds by the induction hypothesis. The drawing of the - th root ends the induction proof.

This proof can be found for example in the textbook on analysis of H. Heuser, Part 1, Chapter 12.2.

Evidence from the rearrangement inequality

A non- inductive proof of the inequality of the arithmetic and geometric means, which does not require logarithmic function, can be carried out with the help of the rearrangement inequality. From the rearrangement inequality it follows that for positive numbers and any permutation of the relationship

Must apply. If, specially

So it follows

From which the inequality follows directly from the arithmetic and geometric means.

Generalizations

Inequality of the weighted arithmetic and geometric means

For a given positive Gewichtstupel with and sum with

The weighted arithmetic mean and

The weighted geometric mean called. Also for these weighted means applies the inequality

The proof follows directly from the above proof with the jens between inequality.

For, with and with obtaining the Young's inequality

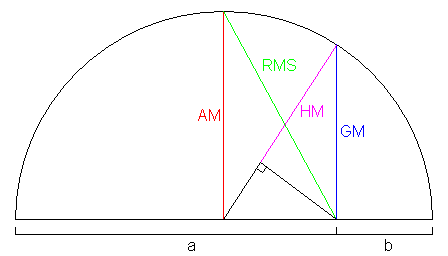
Inequality of the harmonic and geometric means

If one requires strictly greater zero and replaced in the inequality of arithmetic and geometric means by, we obtain the inequality of the harmonic and geometric means:

This inequality is also valid for the weighted mean:

Inequality of generalized means

As Hölder with exponent means is referred to the expression

• For obtaining the arithmetic mean,
• The limit yields the geometric mean.

In general, for the generalized Mittelwertungleichung:

This inequality can for example be prove, by setting and and the Hölder 's inequality with uses, or by applying the Jensen's inequality for the convex function on the values.

Also, this inequality is also true for the weighted mean: Be

With the weighted mean with exponent of the numbers, then for - ∞ ≤ s ≤ t ≤ ∞, the inequality:

This inequality can also be from the Hölder 's inequality to prove by putting you as well, or also by applying the Jensen's inequality for the convex function on the values.

Transferred to integrals over the measure space with a finite measure takes the inequality of generalized means the form

To; in particular it follows that for these spaces.