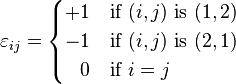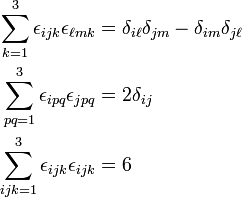Levi-Civita-Symbol

The Levi- Civita symbol, also Permutationssymbol, ( a little careless ) called totally antisymmetric tensor or epsilon tensor, is a symbol that is useful in the vector and tensor calculus in physics. It is named after the Italian mathematician Tullio Levi -Civita ( 1873-1941 ). Looking in mathematics generally permutations people speak instead of the sign of the corresponding permutation. In differential geometry one considers the independent coordinates Antisymmetrisierungsabbildung and the Hodge star.

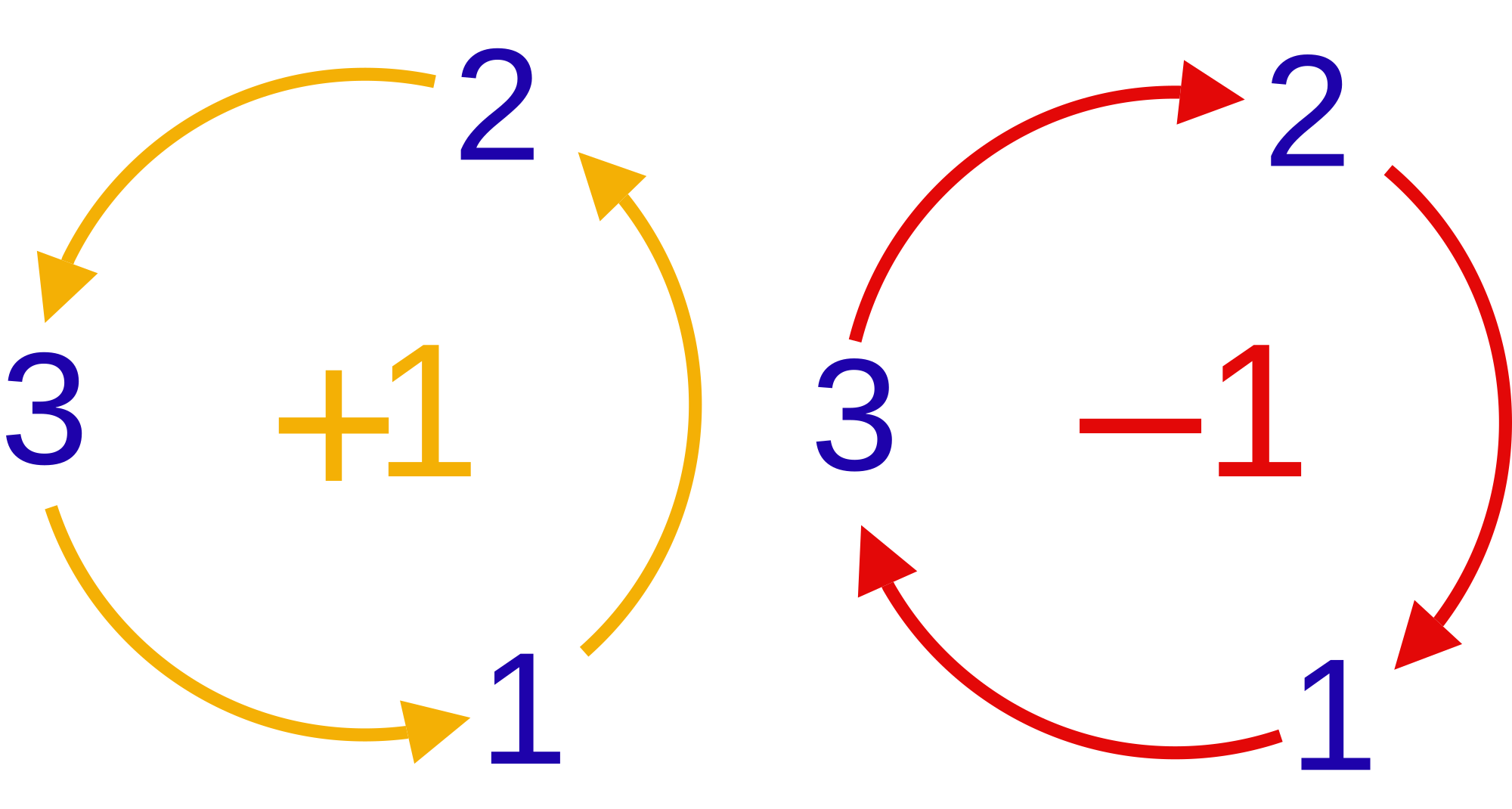
The indices to have values ​​from 1 to. If two indices the same value as is. Are the values ​​of the indices pairwise different, so the icon indicates whether an even () or odd () number of permutations of the indices is necessary to arrange the values ​​in ascending order. For example, since a permutation is necessary to bring in the order of 132 123.

• 4.1 Vector Analysis
• 4.2 Theory of Relativity
• 4.3 Quantum Mechanics

Definition

The Levi- Civita symbol in n dimensions has n indices from 1 to n usually run ( for some applications even from 0 to n -1). It is defined by the following properties:

• .
• Under interchange of two indices changes the sign.

From the second property immediately follows: If two indices are equal, the value is null.

Equivalently, the definition

An alternative definition is used a formula that is also used to represent the sign of a permutation:

Denote the set of natural numbers from 1 to. It is the Levi -Civita symbol as an illustration conceive with, if it is not bijective, otherwise ( ie the sign of, if a permutation is ).

Related to the determinant

The determinant of a matrix can be written with the Levi -Civita symbol and the summation convention as follows:

More generally, the relationship

Substituting into this relation for the unit matrix, ie for the Kronecker delta, we obtain the following representation for the Levi -Civita symbol:

The rows of the matrix are the unit vectors of the standard basis of. This matrix is thus that permutation matrix which maps to the vector. This is obtained by using the product rule for determinants of an expression for the following tensor:

Using the Laplace expansion theorem, one obtains the following relationship when one tapered over the first indices in each of the two tensors:

Specifically in three dimensions,

The Levi- Civita symbol can be represented as a triple product of three orthogonal unit vectors:

When the product of two epsilon tensors advantage is taken that the product of two determinants can be written as a determinant of the matrix product. In addition, one uses the identity of the determinant of a matrix and the determinant of the transposed matrix:

Thus, the product of two epsilon tensors can be written as a determinant of Kronecker deltas:

As components of a Pseudotensordichte

If we define a covariant Pseudotensordichte times the weight -1, by specifying for a given ordered basis of and all its components through, so do not change the components of this Pseudotensordichte in a change of basis. In this sense, therefore, represents the Levi- Civita symbol with respect to arbitrary bases, the components of a Pseudotensordichte, justifying follows in particular that the symbol describes the components of a tensor, if we consider only orthonormal bases of positive orientation.

Similarly, the Levi- Civita symbol are used to define the covariant totally skew-symmetric tensor field of a -th component, called a differential form, used in or on a general -dimensional orientable semi- Riemannian manifold. Such a differential form is only determined up to a scalar factor. The choice of the prefactor fixed unit volume and defines the differential form as a volume form. In the Euclidean space is the Levi- Civita symbol for the components of the standard volume in the standard basis. With regard to another base, the same tensor has evidently the components, and its inverse matrix. If the base is not orthonormal with respect to the Standardskalarprodukts, then differ according to co- and contravariant components of the tensor. The pre-factor depends on the coordinates if curvilinear coordinates are used or the base is a space underlying ( orientable ) manifold. For a semi - Riemannian manifold with metric tensor and the associated Riemannian volume form (see Hodge star operator) the pre-factor is given by. The sign depends on the selected orientation. The relationship between Levi- Civita symbol and Kronecker delta generalized to be

Applications

Vector Analysis

For the three-dimensional case, it follows

Said.

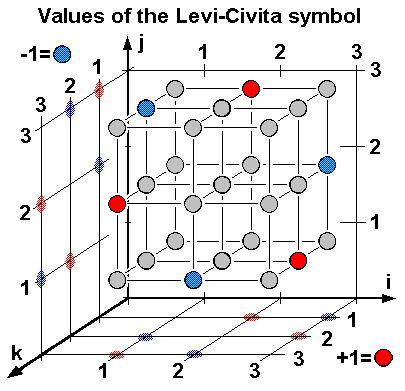
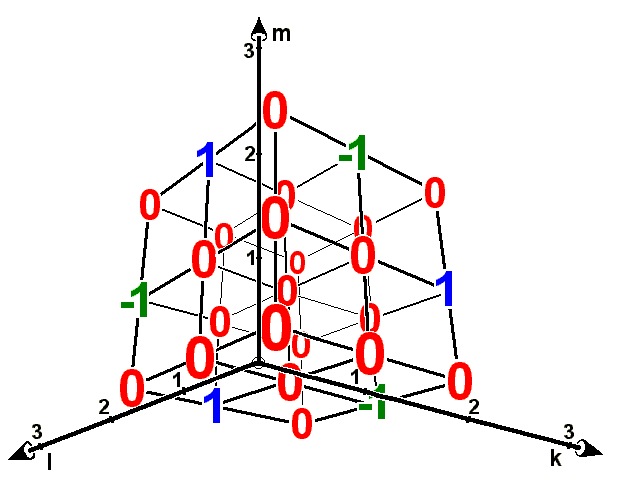
As shown in the adjacent figure, there are only 6 of the 27 non-zero components:

In this example, one further recognizes an invariance under cyclic permutation of the indices, however, only applies if n is odd - is not the case, is a cyclic permutation of the indices with a sign change associated.

The following numerical example demonstrates the representation as a determinant, which can also be expressed by the scalar triple product in the three-dimensional case:

The Levi- Civita symbol with three indices proves in vector calculus useful to write the components of the cross product of two vectors. It is

In such calculations, the Einstein summation convention is often used, that is, letting the summation sign away and agreed that over twice occurring indices in products will always automatically adds:

Is the -th unit vector, then this equation can be written as:

For the scalar triple product

In this respect the properties of the Levi -Civita symbol is clear as components of a volume form, as the triple product is equal to the volume of the plane defined by the three vectors Spates.

For the relationship between Levi- Civita symbol or epsilon tensor and the Kronecker delta we obtain the relationship

From this follows (again with summation convention )

These relationships are useful in the derivation of identities for the cross product.

Furthermore, the epsilon tensor assigns a vector of a skew-symmetric matrix with. So that the cross-product can be expressed as matrix product. In mathematics, this assignment is called the Hodge star operator. An example is the mapping of the magnetic field vector corresponding to the components of the electromagnetic field tensor. Such an association is also known for other axial vectors, such as for the angular momentum vector, as usual.

Relativity theory

In the theory of relativity must be between co- and contravariant components of the epsilon- tensor distinction. In the following, defined in four-dimensional Minkowski space, the signature of the metric tensor as (1, -1, -1, -1). The indices should have values ​​from 0 to 3. It should also be set for the four-fold contravariant component. Different authors use different conventions for the signs in metric and epsilon tensor. As usual, indices are moved with the metric tensor. Is then obtained, for example, for the four-fold component of covariant.

The epsilon tensor remains invariant under proper Lorentz transformation:

This follows directly from the fact that the determinant of is 1. The epsilon tensor can be used to define the dual electromagnetic field strength tensor, by means of which, in turn, noted down the homogeneous Maxwell equations compact.

An application of the two-stage epsilon tensor in the theory of relativity arises when one maps the Minkowski space to the vector space of Hermitian matrices. Here are the Pauli matrices and the negative unit matrix. Correspondingly, the assignment of tensors. The metric tensor is mapped to the product of two epsilon tensors. In this formalism are objects with an index spinors and the Epsilon tensor plays the same role on the translation of ko - in contravariant components of the metric tensor as in ordinary Minkowski space. This formalism is known under the name of van der Waerden - notation. For the metric is usually the signature ( -1,1,1,1 ) is selected. Applies, where the definition for the epsilon tensor.

Quantum mechanics

In quantum mechanics, the Levi- Civita symbol is used in the formulation of the angular momentum algebra. Expressed in mathematical terms match the symbol with the structure constants of the Lie algebras. The following example illustrates the use of the Levi -Civita symbol in this context. The Lie algebra can be used as the sub- algebra of skew-symmetric matrices, that is, are the real matrices shown. The generators (base) of the matrices is given by, with the components. The commutators of the generators can then be written.