Linear congruential generator

The congruence form a class of algorithms that generate random -looking sequences. The numbers thus generated is called pseudo-random numbers are because they are generated deterministically and thus are not truly random. Congruential generators are the best known and most commonly used recursive arithmetic random number generators.

General congruential

A congruence is defined by the following parameters:

• The number of state values
• Module
• Factors
• Increment
• Initial values ​​( seeds, engl. "Seed " )

For it is now

The thus calculated are used as random numbers. Do you need random real numbers in the interval, so you can ensure the approximation

Using, if the module is large enough to provide a sufficiently fine division.

The state of the generator prior to the generation of is given by the values. This condition sets (when given ) fixed all subsequent random numbers since the next random number and the next state are determined by the current state. There are possible states, and therefore to an earlier state must be renewed within steps. The congruential thus produces a periodic sequence of numbers, the period length can be as much smaller. In extreme cases, it is 1, and the generator always generates the same " random" number. In the definition of the parameters therefore occurs in, inter alia, ensuring a sufficient period length.

Linear congruential

With one obtains the special case of a linear congruential. When it is called a multiplicative congruential generator, and for non- linear mixed congruential.

The latter is more frequently used and has four integers as parameters:

• Module
• Factor
• Increment
• Starting value

Then the other values ​​are calculated using the following formula ( with ) from the starting value:

The linear congruential generator was introduced in 1949 by DH Lehmer. It is used in the runtime libraries of programming languages ​​for generating pseudo- random numbers. In cryptography, however, he is not used, because you can, and thus calculate the parameters and the complete sequence of numbers already from a few values ​​of the sequence of numbers generated.

Period length

Linear congruential generators is just the set of Knuth iff its maximum possible period length if the following conditions are met:

• The increment is relatively prime to the modulus.
• Each prime factor of shares.
• When is divisible by 4, then.

In this case, the generator generates any number from 0 to exactly once and then starts over again. It thus provides a pseudo-random permutation of these numbers. The start value can be any number from this set.

The multiplicative congruential generator ( with ) thus has a period length as have smaller. The set of Carmichael states that for a given period of its length is exactly at a maximum when the following applies:

• Must be relatively prime,
• Is a primitive element modulo.

For some special cases of the primitive elements modulo can be easily determined:

• Is a power of two, then you have mod 8 provide the rest of 3 or 5. The period length is then, and the start value must be odd. There are two cycles, each comprising half of the odd numbers up.
• If m is prime, then it must apply to all prime factors of: . Then is the period length. The start value can not be null.

Shortcomings of numbers generated

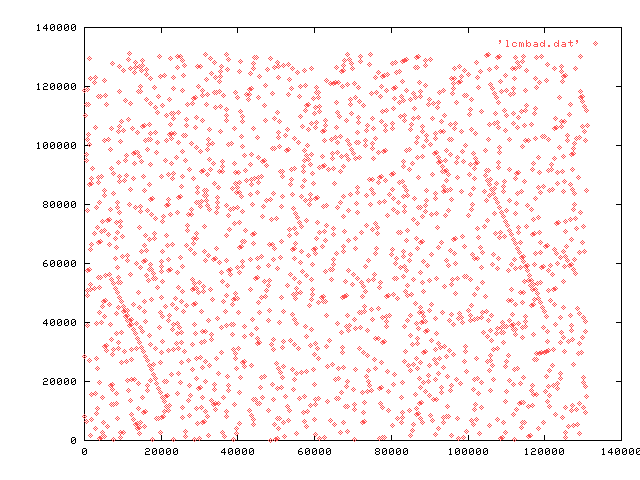
The linear congruential generator does not provide completely randomly appearing numbers. It can be shown that a dependency of consecutive numbers is.

Sub-period

Often one chooses, the word length of the computer in bits, because then you do not have the modulo division calculated explicitly. It arises by itself by cutting off the overflow bits. In this case behave the least significant bits of the condition number as a generator to the module. Thus, these bits are repeated at the latest steps. This means in particular that the least significant bit at best, has the period 2, so changes regularly between 0 and 1. A multiplicative congruential it is even constant.

In general, for all linear congruential generators: if a divisor of the module is then given a series of numbers with the period:

If the generator according to the set of Knuth has period, then the length of the sub-period is exactly for all divisors of.

Because of this partial period behavior, it is inconvenient to win by random numbers, if not and are relatively prime. Then the remainder of the division for a number and divides, a period of length would go through a maximum. If you want for example to simulate a six-sided die and straight, then provides numbers that are even and odd turns.

Possible remedy:

• One uses a multiplicative congruential generator with a large prime number as a module and sets. But then, the non- uniformly distributed, unless a multiple of. If it is, then the deviation from the uniform distribution is only slight.
• It sets and applies the most significant bits of a rejection method. The bits are shifted to the right, the smallest power of two. It is used only, the rest are discarded. This method yields uniformly distributed results.

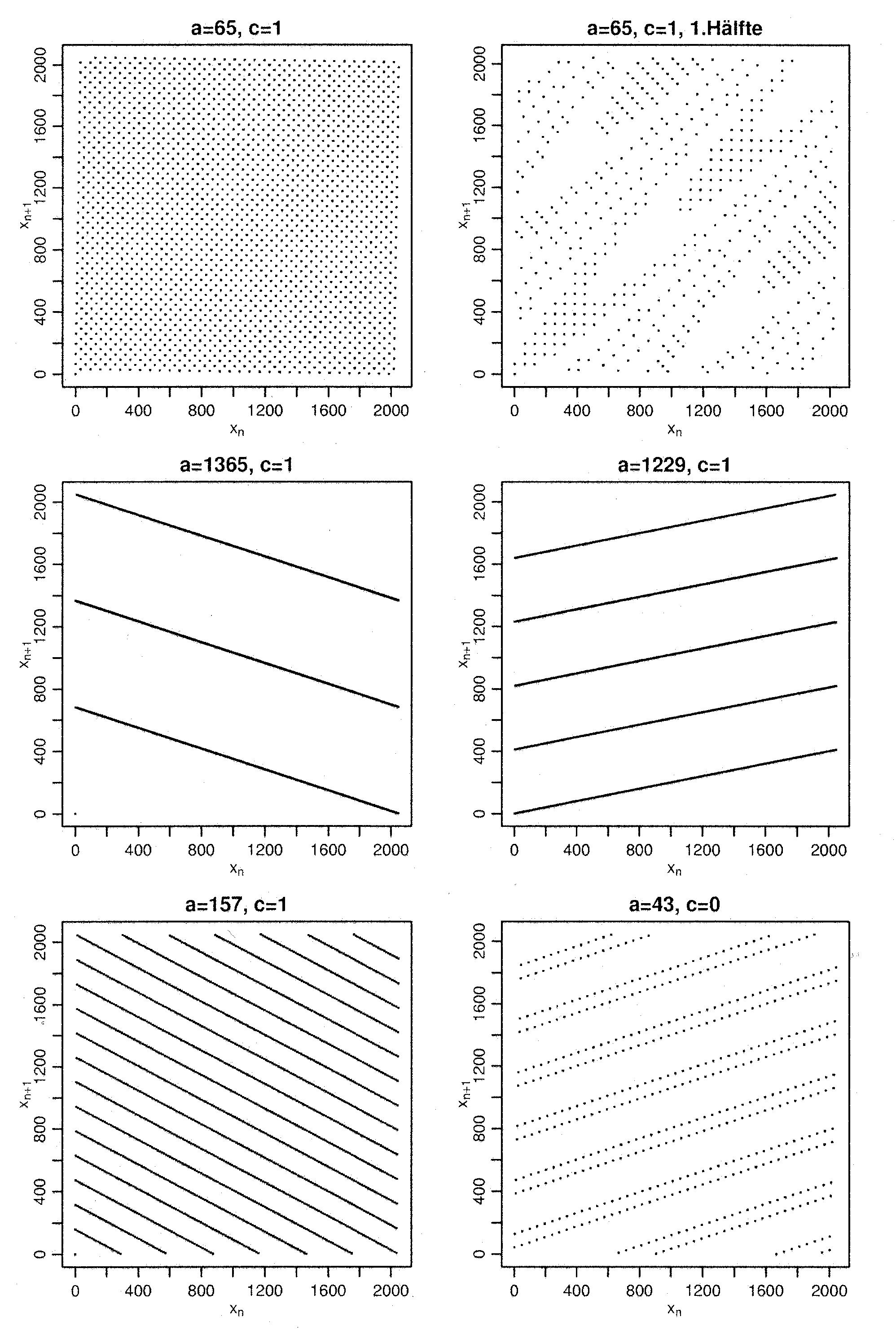
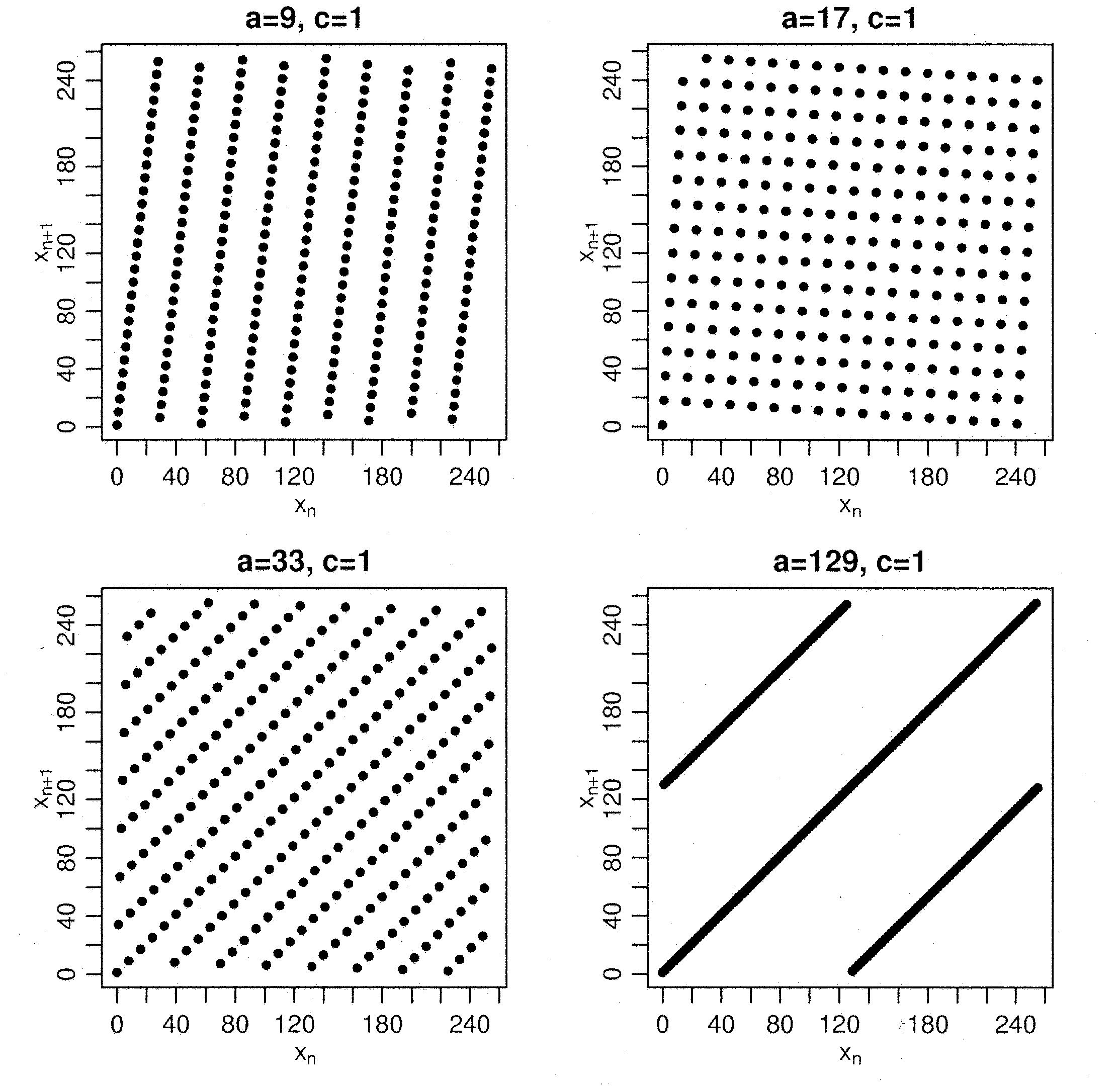
Hyperplanes behavior

The linear congruential generator has a hyperplane behavior, see set of Marsaglia. By suitable choice of the parameters, and can optimize the performance of the generator and to achieve a large number of hyperplanes. Given you can make the following rules of thumb:

• Should neither be too large nor too small, such as:
• Should be a "round" number are chosen as random as possible, so not in dual or decimal form.
• In a mixed linear congruential the potency should be as large as possible. It is the minimum value for which is a multiple of. Donald Knuth recommends that the potency should be at least 5. If so, should be, in order to obtain the maximum potency.

If you want to make sure that the generator produces good random numbers, you should not rely solely on these rules of thumb, but check the generator with the Spektraltest.

Because of the hyperplanes behavior are accessed instead of the linear congruential occasionally inverse congruential back which does not have this problem. However, it requires a higher computational effort. He is not a special case of the general congruential.

Fibonacci generator

A Fibonacci generator is also a congruence ( with, and ) and consists of the following components:

• Module
• Starting values

It should be.

With the following formation rule, the pseudo-random numbers are generated:

One characteristic is that the cases or never occur. Fibonacci generators are therefore not suitable as a pseudo random number generators. This applies particularly to mathematical objects for which more than two random number generating required. If, for example, so try to generate a random cloud of points in a cube, so would all the points lie on two levels.

Delayed Fibonacci generator

The principle of the Fibonacci generator can also be generalized by using not the last, but further back in two state values ​​to generate the new random number. This results in a delayed ( engl. ' lagged ') Fibonacci Generator:

Then and therefore, the rest are zero. Here one chooses just generally and so that the polynomial in x

A primitive polynomial modulo 2. Then the period length of the generator is at least.

The following table gives some values ​​for pairs and that meet this condition:

Is exactly then a primitive polynomial modulo 2, if this is true for. Thus, one can use instead of always.

This generator is also used in practice. But he also does not provide completely random appearing numbers. The problem of simple Fibonacci generator is only shifted: it has never or. In addition, there are other defects.

As a remedy, it has been proposed to use only sequential numbers, and then discard the next to numbers. This works fine, but at the price of 5 to 11 times higher computational complexity. Proposed by Donald Knuth generator ranarray works this way. Is with him and, and of 1009 consecutive numbers only a block of 100 numbers is always used.

To ensure the period, it just depends on the least significant bit in each of the state values ​​, ie, whether they are even or odd. The high order bits may be modified as desired in order to improve the quality of the obtained random numbers. For example:

Other

One can generalize the Fibonacci generator further delayed by processing more than two state values ​​:

Is the largest element in here. In order to guarantee a period of at least, the corresponding polynomial must also

A primitive polynomial modulo 2 (with a straight module). A so constructed generator with generally provides better random numbers than with, but again at the cost of higher computational complexity.

With a further generalization can be for a given increase the period length and probably also improve the quality of random numbers on. was a prime factor of. for the calculation rule

Are the so chosen with that the polynomial in x

A primitive polynomial modulo p. Then, the period length is at least. The previous generator arises from the fact and with a special case and provides a multiplicative congruential generator with period length.

The polynomial is a primitive polynomial modulo p if the following conditions are met:

()

• Is a primitive element modulo p
• The polynomial is congruent to (modulo )
• For all prime factors of the degree of the polynomial is positive

In this case, polynomial arithmetic is applied (see polynomial and polynomial ), and the coefficient is calculated modulo (they are the elements of the residue class ring ).