Linear span
In linear algebra, the linear span (also the tension, Span [ from English ], clamping or final called ) to a subset of a vector space over a field, the set of all linear combinations of vectors from scalars from. The linear hull forms a subspace, which is also the smallest subspace that contains.
Definition
Constructive definition
Is a vector space on a body and a portion of the vector space, then
The linear span of. The linear case, the set of all linear combinations of the finite.
In the case of a finite subset of this definition simplifies to
The linear span of the empty set is the zero vector space, that is
Because the empty sum of vectors gives by definition the zero vector.
Other definitions
Equivalent ( equal) to the structural definition of the following definitions:
- The linear span of a subset of a vector space is the smallest subspace that contains the amount.
- The linear span of a subset of a vector space is the intersection of all subspaces of containing.
Notation
Properties
Be two sets of subsets of the K- vector space. Then:
These three properties characterize the linear hull as a closure operator.
Next apply:
- The linear span of a subset of a vector space is a subspace of.
- For every subspace of a vector space.
- A set of vectors is a generating set of their linear span. In particular, if a set of vectors a generating set of a subspace, so this is their linear span.
- The sum of two subspaces is the linear hull of the union, ie.
- In the set of subspaces of a vector space (including the total area ), you can the operation " constitutes the linear hull of the union of " two-digit shortcut introduce. The corresponding dual link is the intersection of education. With these links then forms a lattice.
- Are subspaces of a vector space, then for the linear dimensions of the shell and the intersection of the formula:
Examples
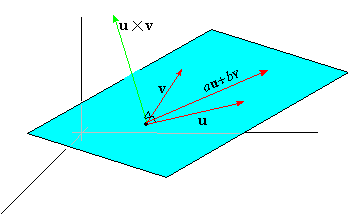
- The linear span of a single vector is a straight line through the origin.
- The two vectors and are elements of the real vector space. Their linear span is the - plane.
- Be the vector space of formal power series to the body and the amount of the monomers. Then the linear span of the subspace of polynomials: .