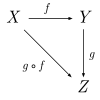Morphism

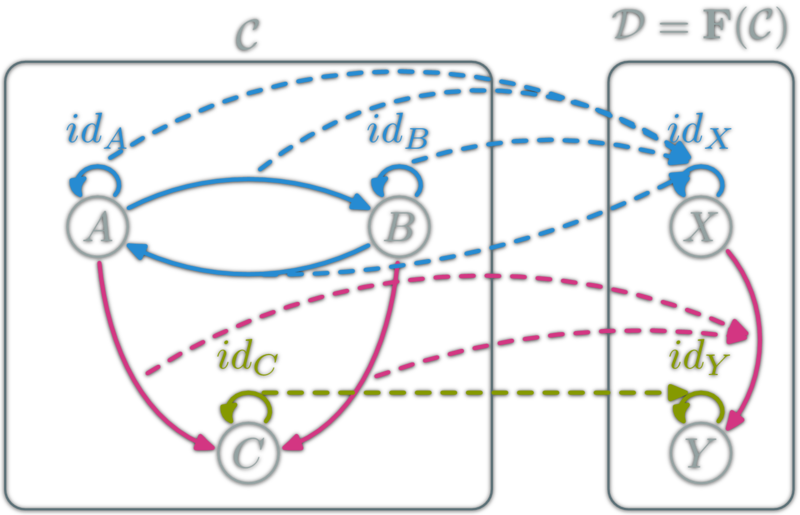
In category theory ( a branch of mathematics ) one considers so-called ( abstract ) categories, which are respectively given by a class of objects and for each pair of objects and a class of morphisms from to (also called arrows).

One writes:

Heard a partial linkage of morphisms, which must meet certain conditions to the category.

If one interprets quantities with the same structure as objects and functions between the underlying quantities that are compatible with their structure, as appropriate morphisms, then one speaks of a specific category. Linking the morphisms then corresponds to the usual sequential execution of functions. But there are also quite different from formed concrete categories where morphisms not occur as functions between the objects, ie the category Toph, whose objects are topological spaces and whose morphisms are homotopy classes of continuous functions, or the category Rel whose objects are sets and whose morphisms the amount of the relations between two objects are.

Examples

Concrete examples of morphisms are homomorphisms of categories that are studied in algebra (eg groups or rings), continuous functions between topological spaces, differentiable functions between differentiable manifolds.

Each quasi-ordering defines a category in which the objects are the elements of and a morphism exists if and only if.

• A homeomorphism is an isomorphism between topological spaces.
• A diffeomorphism is an isomorphism between differentiable manifolds.
• A linear mapping is a ( homo) morphism between vector spaces.

Types

• Each object of a class has an identical morphism written, which is for all morphisms a fairly neutral element and for all morphisms a left identity element of the composition, so that always and is.
• If a morphism has a right inverse, ie if there is a morphism, then called retraction. Analogously, one designated section ( section Core traction ) is a morphism which has a left inverse.
• Is both a retraction as well as a section, then called isomorphism. In this case the objects and are considered to be alike within each category can ( isomorphisms for example, in the specific category of sets the bijective pictures).
• A morphism of endomorphism by means of
• An endomorphism which is an isomorphism at the same time, is called an automorphism.
• A morphism with the following property is called epimorphism: Are any morphisms with, then it is always (for example, every surjective homomorphism is an epimorphism ).
• A morphism with the following property is called monomorphism: Are any morphisms with, then it is always (for example, every injective homomorphism is a monomorphism ).
• An epimorphism is called extremal if from and is a monomorphism, always follows is an isomorphism.
• A monomorphism is called extremal if and is an epimorphism, always follows is an isomorphism.
• Is both an epimorphism and a monomorphism, then a Bimorphismus. Not everyone Bimorphismus is an isomorphism. However, it is every morphism is an isomorphism, and the epimorphism section, or monomorphism and retraction is. An example of a Bimorphismus which is not an isomorphism, which provides embedding of the integers in the rational numbers as homomorphism of rings.

• Category theory