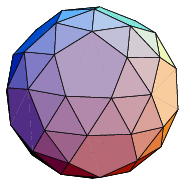
Snub dodecahedron

The chamfered dodecahedron ( Dodecaedron simum ) is a polyhedron, which is one of the Archimedean solids. It is composed of 92 surfaces, namely 12 regular pentagons and 80 equilateral triangles together and has 60 vertices and 150 edges. In each case, four triangles and a pentagon form a corner of the room.

The following pictures show two mirror -image bevelled dodecahedron.

Mirror variant 2

The dual to the chamfered dodecahedron body is the Pentagonhexakontaeder.

Construction

• As the name suggests, this polyhedron is produced by continuously chamfering a dodecahedron, so that at the end of twelve (smaller ) regular pentagons remain, which are coincident with the original boundary faces of the dodecahedron.

• You Twisted at a rhombicosidodecahedron all twelve pentagons - which are coincident with the boundary surfaces of a circumscribed dodecahedron - each to the same given angle and adds a diagonal in the now distorted square one, creates a sloping dodecahedron.

Formulas

Subsequently, the term designates the cosine of the smaller central angle in Sehnenfünfeck (see chart above right) with the side lengths and ( is the diagonal in the Pentagon, the golden number ).

Is the only real solution of the cubic equation.

Comments