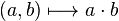Topological algebra

A topological algebra is a mathematical structure. Is an algebra, usually over the field of real or complex numbers, which carries a topology such that the algebraic operations, that is, the addition, the multiplication and the scalar multiplication are continuous. Such algebras whose most prominent representatives are Banach algebras are studied in functional analysis.

• 3.1 Q- algebras
• 3.2 algebras with continuous inverse

Definition

A topological algebra is an algebra, so that the images

Are continuous. making a topological vector space in which a constant multiplication is defined.

Important classes

Banach algebras

The most common examples are normalized algebras, especially Banach algebras. Particularly for the latter an extensive theory has been developed. Important special cases are C *-algebras, in particular von Neumann algebras and group algebras in harmonic analysis.

Fréchet algebras

This is to algebras which form a sequence with respect to submultiplikativer seminorms a Fréchet space. The Submultiplikativität the semi-norms ensures the continuity of the multiplication.

The algebra of all continuous functions on a separable, locally compact Hausdorff space is a Fréchet algebra if the topology by the semi-norms

Defined, with a sequence of compact sets is located on the inside of and comply. then transmits the topology convergence of the compact, and is therefore also referred to as.

Specifically, is an open set, so is the algebra of holomorphic functions a sub - Fréchet algebra. These algebras are not normalizable, so no particular Banach algebras, they play a role in the theory of functions of several variables.

LMC - algebras

An LMC -algebra or locally multiplicatively -convex algebra is an algebra with a locally convex topology defined by a family submultiplikativer seminorms. The Submultiplikativität ensures the continuity of the multiplication. The full LMC - algebras are also called Arens- Michael algebras, they can be investigated using the Arens- Michael decomposition.

Be a topological space and the algebra of continuous functions with the topology of pointwise convergence. This is of the family of standards submultiplikativen half, wherein defined. Is uncountable, so is not a Fréchet algebra.

Locally convex algebras

A topological algebra is called locally convex algebra if its topology is locally convex. By definition, LMC - algebras is locally convex, but the topology of a locally convex algebra is not necessarily generated by a family submultiplikativer seminorms.

As an example we consider the algebra, the quotient field of the polynomial ring. We define functions

Each element can be considered as a function of a complex variable, and as such has a Laurent development. Now, define the seminorm on by

One can show that the semi-norms is a locally convex algebra which is not a LMC - algebra.

Properties

Important properties of Banach algebras transferred not to more general classes. So is the automatic continuity of homomorphisms of the algebra in the body, which is given in Banach algebras, in Fréchet algebras an open problem. Other typical properties of Banach algebras are to be claimed in addition to more general situations. This then leads to further classes of algebras.

Q- algebras

A topological algebra with identity element is called Q- algebra if the set of invertible elements is open. A topological algebra with identity is precisely then a Q- algebra if the inside of is not empty. The spectrum of an element of a Q- algebra, that is, the amount is compact.

Every Banach algebra is a Q- algebra, the Fréchet - algebra is not a Q- algebra.

Algebras with continuous inverse

Is in a topological algebra with identity the picture constantly, they say, is an algebra with continuous inverse. The above example of a locally convex algebra has no continuous inverse. It is by means of the Arens- Michael decomposition show that LMC - algebras have continuous inverses.