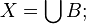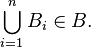Bornological space

Bornological spaces are in the mathematical branch Functional Analysis special locally convex spaces for which linear operators applies the well-known from the theory of normed spaces equivalence of continuity and boundedness. These spaces can be characterized by their zero neighborhood bases and have additional properties with normed spaces together.

Motivation

A subset A of a topological K- vector space E is called bounded if it is absorbed by every neighborhood of zero, ie every neighborhood of zero, there is a with.

A subset B of a locally convex K- means Vektorrraums Bornolog if the following conditions are met:

• B is absolutely convex, that is, applies for and with.
• B absorbs every bounded set, that is, every bounded set, there is a with.

Easy, one can show that every locally convex space has a base of neighborhoods of Bornologen. Conversely, if each Bornolog a neighborhood of zero, it is called the space bornological.

Examples

• Every metrizable locally convex space E is bornological. Indeed, if B is a Bornolog in E, a countable base of neighborhoods of e, and assuming that B does not contain any set of the form, so you can choose one. Then converges, that is, is compact and therefore limited, so in an amount of form. For the contradiction follows. So B is a neighborhood of zero.

• If E is a normed space than { 0}, then with the final topology is an example of a bornological space which is not metrizable.

Inheritance properties

An Inductive limit bornological spaces is bornological again.

Bounded operators

As in the theory of normed spaces is called a linear operator between topological vector spaces bounded if it maps bounded sets to bounded sets again.

Are equivalent for a locally convex space E:

• E is bornological
• Every bounded operator in another locally convex space F is continuous.

A linear operator is called sequentially continuous if for always follows in E in F. In non- metrizable spaces, this condition may be genuine weaker than continuity.

Are equivalent for a bornological space E and a linear operator:

• A continuous.
• A is sequentially continuous.
• A is bounded.

Bornological spaces as inductive limits of normed spaces

A locally convex space E is called an inductive limit of normed spaces if there are linear maps with normed spaces, and so the topology on E is the finest locally convex topology that makes all steadily.

Are equivalent for a locally convex space E:

• E is bornological.
• E is an inductive limit of normed spaces.

You can even specify such an inductive limit. Is for a limited and absolutely convex set. Then is a vector space, and the Minkowski functional to make this vector space to a normed space. The locally convex space is bornological if and only if it carries the inductive locally convex topology of all inclusions, with the limited, absolutely convex sets by running.

Can you even find a representation for E as inductive limit of Banach spaces, it is called E ultrabornologisch. In such areas, the phrase on the open image and apply the principle of closed graph.

Completeness of the dual space

If E is a locally convex vector space, defined every bounded set B in E is a semi-norm on the dual space by setting. Provided with the amount of semi-norms, where B runs through the limited quantities of E is a locally convex vector space, then the one designated. This generalizes the dual space formation in normed spaces. As in the theory of normed spaces, the following sentence is true:

If E is bornological, so complete, that is, every Cauchy net converges.