Brusselator

The Brusselator is a simple model for the description of chemical oscillators. The Brusselator was developed by Ilya Prigogine and René Lefever at the Université Libre de Bruxelles in Belgium, hence the name.

Description

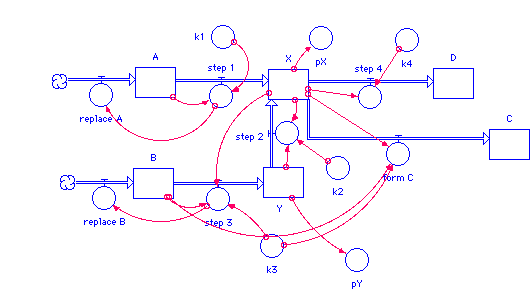
It is a system of four hypothetical reaction equations, which form a simple model that reflects all phenomena of chemical oscillators (such as the Belousov -Zhabotinsky reaction). A similar model system was derived in 1995 at the Humboldt University in Berlin by simplification from a real existing reaction system.

The reaction rates are reflected by the constant K1 to K4. The concentrations of A and B are always kept constant, and the C and D can be continuously discharged. The concentrations of X and Y are sensitive to small perturbations and quickly reach an oscillating state when the overall reaction is far from equilibrium. So you have a thermodynamically open system and can set up two rate equations for the concentrations of X and Y:

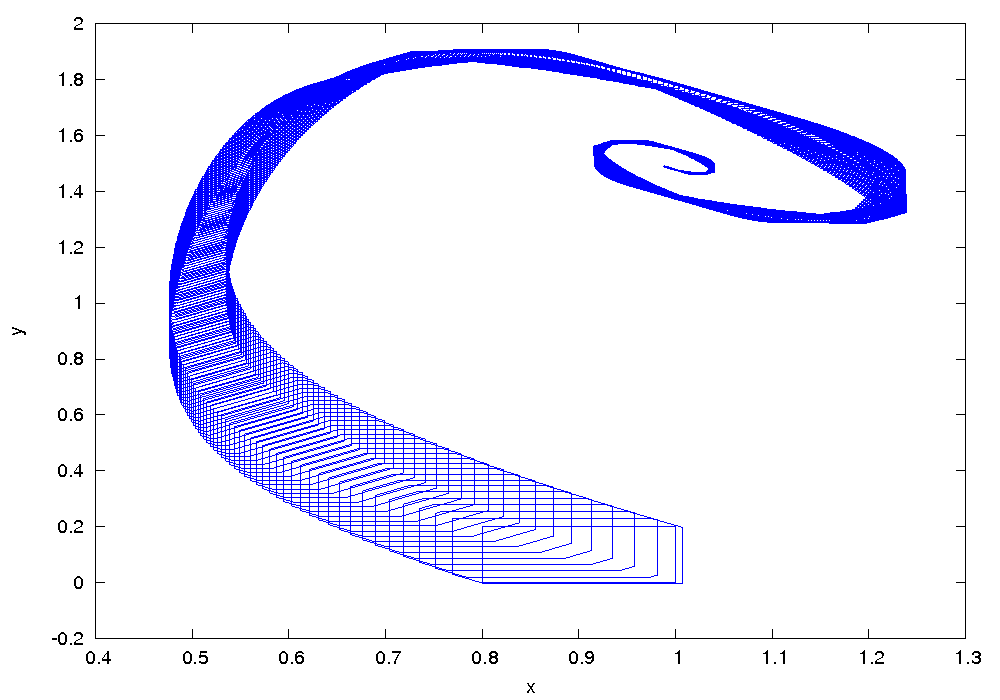
These differential equations can be solved numerically. The diagram opposite shows some solutions. Depending on the choice of the free parameters K1A, K2B, k3 and k4 results in different behavior. The upper case can be seen stable oscillation, while for a different choice of the parameters the concentration X (t) and Y (t) approach a fixed point in the phase space.

Stability analysis

As already shown in the above image, the Brusselator, depending on the parameterization stable oscillations as a solution or aims in phase space to a fixed point. The fixed point results on dX / dt = dY / dt = 0:

Using the linear stability analysis can be further show that this fixed point is unstable if:

In this case, the trajectories (X (t ), Y ( t)) of seeking a limit cycle in phase space, and the system executes the oscillations shown in.

Brusselator as a reaction-diffusion model

One can also extend the model to a reaction-diffusion model, and then gets in choosing the right parameter Chemical waves as a solution, as shown in the animation on the right.

The differential equations are extended to include a diffusion component, respectively, and then read:

Herein is a point in space, and denotes the Laplace operator, that is, in Cartesian coordinates, the sum of the second spatial derivatives.