Cantor distribution

The Cantor distribution is a probability distribution which is singular with respect to the Lebesgue measure. The corresponding distribution function is called the Cantor function or devil staircase.

Construction of the Cantor distribution

The Cantor distribution ( with Borel σ - algebra as ) can not be simply stated explicitly. It must be recursively constructed similar to the Cantor set.

First variant of the construction

Assuming the uniformly distributed on the measure amount is obtained on the amount of a product dimension. This measure can be interpreted as follows: One considers an experiment in the infinitely often a fair coin is tossed; Elements can be used as outputs of the experiment interpret ( the result means, for instance, that always turns heads and tails have occurred). The measure has a subset of now to their probability. For example, says the strong law of large numbers, that the amount of " uniformly distributed " Follow probability 1, said the following amount:

Now can the Cantor set C - as stated in the local products - bijective on map. The above measurement can be by virtue of this bijection transferred to a probability measure on the Cantor set. ( An alternative description of results as the Hausdorff dimension to. )

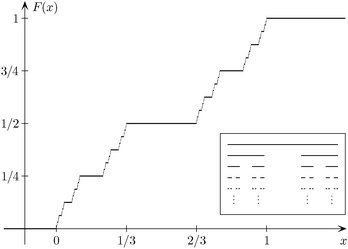
This probability is the Cantor distribution, an example of a measure of the distribution function is continuous but not absolutely continuous. The distribution function

Called Cantor function (also called " Cantor staircase function"). On each interval in the complement of the Cantor set, this function is constant; on the interval has, for example, the value 1/2, and in the interval it is set to 1/4.

Second variant of the construction

In this design, the Cantor function is constructed, which is uniquely determined by the correspondence set the Cantor distribution.

Be the system of all subsets of which can be represented as the union of finitely many disjoint closed non-empty intervals. Furthermore, it is given by ( with )

( This corresponds to the already mentioned recursive trisection of the intervals (interval - length: bi -ai ), wherein only the lower and upper thirds taken during the middle third " wiped out " is. )

Be still with

Finally, the Cantor set is defined by

Now, the measurement is defined as follows:

Where the one-dimensional Lebesgue measure called. is obviously a probability that is associated distribution function. For the following applies:

For especially and.

Since is uniformly convergent, the Cantor function is by

Clearly defined. The corresponding distribution in the sense of measure theory is the Cantor distribution.

Properties

The Cantor distribution is singular with respect to the Lebesgue measure.
The Cantor distribution is a symmetrical distribution.
The Cantor distribution has no Lebesgue density.
The Cantor function is continuous and monotone increasing between 0 and 1
The Cantor function is almost everywhere differentiable with derivative 0, but not constant.

In the theory of integration thus resulting expressions of the form

A sense, but not expressions of the form

Here, g ( x ) is an arbitrary, in the interval [ 0,1] Lebesgue integrable function.

Physical realizations

Devil Stairs occur approximately in physics in systems with competing length (eg adsorbates or structural phase transitions, which are described by the model of Frenkel and Kontorowa ) or with competing interactions (eg magnets or alloys by the be annni model described ) on.

Discrete multivariate distributions: Ewen | multinomial | Dirichlet compound multinomial

Multivariate matrix distributions: Inverse Wishart | matrix normal | Wishart

Probability distribution

Pictures of Cantor distribution

$Cantor distribution #$

162912