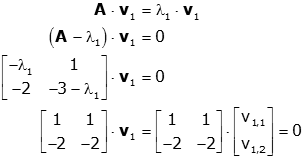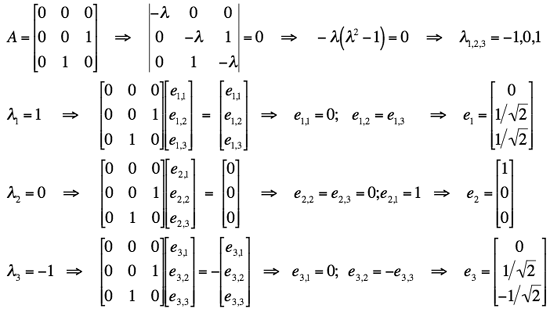Eigenvalues and eigenvectors

Is an eigenvector of an image is different from linear algebra, a zero vector, vector whose direction is not changed by the mapping. An eigenvector is thus only scaled and is called the scale factor as a proper value of the image.

Eigenvalues characterize essential properties of linear maps, such as whether a corresponding system of linear equations has a unique solution or not. In many applications eigenvalues describe physical properties of a mathematical model. The use of the prefix " self - " characteristic quantity in this sense can be traced back to a publication by David Hilbert in 1904.

The mathematical problem described hereinafter called special eigenvalue problem and relates only to linear transformations of a finite-dimensional vector space into itself ( endomorphisms ), as they are represented by square matrices.

The question that arises here is: Under what conditions a matrix is similar to a diagonal matrix?

3.1 algorithm
3.2 Example

7.1 Eigenvalues and eigenfunctions
7.2 Example

Definition

Is a vector space over a field ( in applications most of the field of real numbers or the field of complex numbers ) and a linear mapping from into itself ( endomorphism ), we referred to as eigenvector a vector itself by up to a multiple of itself with mapped is:

The factor is then called the associated eigenvalue.

In other words: Does the equation for a

A solution ( the zero vector is always a solution, of course ), so called an eigenvalue of each solution is called an eigenvector of the eigenvalue

If the vector space is a finite dimensional so every endomorphism can be described by a quadratic. The above equation can then be as matrix equation

Write, where here denotes a column vector. It is called in this case a solution eigenvector and eigenvalue of the matrix

This equation can also be in the form of

Write the identity matrix, and is equivalent to

Reshape.

Calculation of the eigenvalues

For small matrices, the eigenvalues symbolically (exactly ) can be calculated. For large arrays, this is often not possible, so that this method of the numerical analysis are used.

Symbolic computation

The equation

Defines the eigenvalues and provides a homogeneous linear system of equations dar. Since it is assumed this is solvable if

Applies. This determinant is called " characteristic polynomial ". Is a monic polynomial of degree n in its zeroes, so the solutions of the equation

Over are the eigenvalues . As a polynomial of degree n has at most n zeros, there are at most n eigenvalues. Decomposes the polynomial completely, so there are exactly n zeros, where multiple zeros are counted with their multiplicities.

Eigenspace corresponding to the eigenvalue

Is an eigenvalue of the linear mapping then we call the set of all eigenvectors for this eigenvalue associated with the zero vector to the eigenspace corresponding to the eigenvalue, the eigenspace is by

Defined. If the dimension of the eigenspace is greater than 1, so if there is more than one linearly independent eigenvector is the eigenvalue, it is called the eigenspace associated to the eigenvalue degenerate. A generalization of the eigenspace is the main room.

Spectrum and multiplicities

For the remainder of this section is Then every exact eigenvalues , if you count them with their multiplicities. Multiple instances of a particular eigenvalue summarizes and one way, after renaming the enumeration of the eigenvalues with their multiplicities is and will

The multiplicity of an eigenvalue just shown as zero of the characteristic polynomial is called the algebraic multiplicity.

The set of eigenvalues is called and written, so therefore spectrum

Applies. As spectral radius is defined as the largest amount of all eigenvalues.

Applies to an eigenvalue that its algebraic multiplicity is equal to its geometric multiplicity, then one speaks of a semisimple eigenvalue ( from the English ' semisimple '). This corresponds exactly to the diagonalizability the block matrix at the given eigenvalue.

Knowing the eigenvalues and their multiplicities ( the algebraic and further explained below geometrical), you can create the Jordan normal form of the matrix.

Example

Consider the square matrix

Subtracting the multiplied with unit matrix of results

Provides calculating the determinant of this matrix (using the rule of Sarrus )

The eigenvalues are the zeros of this polynomial, we obtain

The eigenvalue 2 has algebraic multiplicity 2, since it is double root of the characteristic polynomial.

Numerical

While the exact calculation of the zeros of the characteristic polynomial is not so easy even for three-row matrices, it is usually impossible for large matrices, so that one is then limited to the determination of approximate values . To this end, methods are preferred, which are characterized by numerical stability and low computational effort. This includes methods for densely populated small to medium sized matrices as

QR algorithm
The QZ algorithm
The QS algorithm
Deflation

As well as specific methods for symmetric matrices, as well as methods for sparse large matrices, as

The power method,
The inverse iteration,
The Lanczos method,
The Arnoldi method,
The Jacobi method and
The Jacobi -Davidson method.

Furthermore, there are still methods to estimate, for example, using

The matrix norm,
The Gerschgorin circles,

Allow always a rough estimate ( under certain conditions even accurate determination ).

The Folded Spectrum Method delivers with each pass an eigenvector but can be derived from the middle of the spectrum.

Calculation of the eigenvectors

Algorithm

For an eigenvalue can be the eigenvectors of the equation

Determine. The eigenvectors span the eigenspace whose dimension is called the geometric multiplicity of the eigenvalue. For an eigenvalue of geometric multiplicity thus can find linearly independent eigenvectors, so that the set of all eigenvectors to be equal to the amount of linear combinations of. The amount is then called a basis of eigenvectors of the eigenvalue associated eigenspace.

The geometric multiplicity an eigenvalue can therefore also be defined as the maximum number of linearly independent eigenvectors for this eigenvalue.

The geometric multiplicity is at most equal to the algebraic multiplicity.

Example

Given is as in the above example, the square matrix

The eigenvalues have been calculated above. First, here are the eigenvectors (and the plane spanned by the eigenvectors of the eigenspace ) calculated for the eigenvalue:

So one has to solve the following linear system of equations:

Brings you the matrix has upper triangular form, we obtain

The desired eigenvectors are all multiples of the vector ( but not the times the zero vector because the zero vector is not an eigenvector ).

Although the eigenvalue has algebraic multiplicity 2, there is only one linearly independent eigenvector ( the eigenspace to the eigenvalue is one-dimensional ); So has this eigenvalue a geometric multiplicity of 1 This has an important consequence: the matrix is not diagonalizable. One can now try to convert the matrix instead in the Jordan normal form. To this end, a further eigenvector must be "forced" to this eigenvalue. Such eigenvectors are called generalized eigenvectors or principal vectors.

For the eigenvalue one goes the same way:

Again bringing the matrix to triangular form:

Here is the solution of the vector is back with all its different from the zero vector multiples.

Properties

Is an eigenvalue of the invertible matrix to the eigenvector as eigenvalue of the inverse matrix of is the eigenvector
If the eigenvalues of the matrix thus applies

Using the eigenvalues , one can determine the definiteness of a matrix. Thus the eigenvalues of real symmetric matrices are real. In terms of the principal axis transformations real eigenvalues of symmetric matrices are also called principal value. If the matrix is strictly positive definite, then the eigenvalues are real and strictly positive.
For a symmetric real matrix can therefore allow us always specify a basis of orthogonal eigenvectors. This is a direct consequence of the spectral theorem. In particular, eigenvectors corresponding to different eigenvalues then mutually orthogonal.
Eigenvectors corresponding to the eigenvalue 1 are fixed points in the figure geometry.
The calculated from the signs of the eigenvalues of a symmetric matrix signature behaves according to the inertia set of Sylvester.
Every square matrix over the field of complex numbers is similar to an upper triangular matrix, the eigenvalues of are exactly the diagonal entries of the matrix
The spectrum of a matrix is equal to the spectrum of the transposed matrix, ie:

Eigenvectors of commuting matrices

For commuting diagonalizable (in particular symmetric ) matrices it is possible to find a system of common eigenvectors:

Commutation of two matrices, and (does so ) and is a non- degenerate eigenvalue (ie, the associated eigenspace is one-dimensional ) of the following applies with eigenvector

So, too, is an eigenvector of the eigenvalue Since this eigenvalue is not degenerate, must be a multiple of. This means that an eigenvector of the matrix.

For this simple proof shows that the eigenvectors to non-degenerate eigenvalues of several pairs of commuting matrices are eigenvectors of all these matrices.

General common eigenvectors can also be found for commuting diagonalizable matrices with degenerate eigenvalues. For this reason, several pairwise commuting diagonalizable matrices can also simultaneously (that is, a basis transformation for all matrices ) can be diagonalized.

Links eigenvectors and generalized eigenvalue problem

Sometimes referred to as an eigenvector defined as a right eigenvector and then defined according to the concept of left eigenvector by the equation

Left eigenvectors are found for example in the stochastics in the calculation of stationary states of Markov chains by means of a transition matrix.

Because the left eigenvectors of just the right eigenvectors of the transposed matrix

Normally, you can also square matrices and and the equation

Investigate. This generalized eigenvalue problem is not considered further here.

Spectral Theory in Functional Analysis

Eigenvalues and eigenfunctions

In the functional analysis (ie, linear maps between infinite dimensional vector spaces ) we consider linear maps between linear function spaces. In most cases one speaks of linear operators instead of linear maps. Be a vector space over a field and with a linear operator. In functional analysis it assigns a spectrum. This consists of all of the operator is not invertible. However, this spectrum is not - as with maps between finite dimensional vector spaces - be discreet. In contrast to the linear maps between finite dimensional vector spaces, which just have different eigenvalues , are linear operators in general infinitely many elements in the spectrum. Therefore, it is possible, for example, that the spectrum of the linear operators has limit points. To simplify the study of the operator and the spectrum is divided is in the range of different partial spectra. Elements to solve the equation for a, it is called as in linear algebra eigenvalues. The set of eigenvalues is called the point spectrum of As in linear algebra is assigned a space of eigenvectors each eigenvalue. Since the eigenvectors are usually understood as functions, one also speaks of eigenfunctions.

Example

Be open. Then the derivative operator has a non-empty point spectrum. If we consider the equation for all

And then selects it is seen that the equation is satisfied for all. So is every one eigenvalue with associated eigenfunction

Practical examples

By solving an eigenvalue problem, we can calculate

Natural frequencies, mode shapes, and possibly also the attenuation characteristic of the oscillatory system,
The buckling load of an articulated rod ( see beam theory ),
The buckling failure (a type of material failure due to insufficient rigidity ) of an empty tube under external pressure,
The principal components of a set of points ( for example, for compression of images, or for the determination of factors in Psychology: principal component analysis ),
The principal stresses in the strength of materials (calculation of stresses in a coordinate system in which there is no shear stresses ),
The principal stretches in the strength of materials as eigenvalues of the deformation tensors,
The principal axes of inertia of an asymmetric cross-section ( one bar - support or similar - in both directions to be calculated independently),
A variety of other technical issues that have to do with each specifically defined stability of a system.
The PageRank of a webpage as an eigenvector of the Google matrix and thus a measure of the relative importance of a website on the Internet
The asymptotic distribution of the Markov chain with discrete state space, and discrete time steps, which are described by a stochastic matrix.

Eigenvalues play a special role in quantum mechanics. Physical quantities such as the angular momentum are here represented by operators. Measurable are just the eigenvalues of the operators. Has, for example, the Hamiltonian representing the energy of a quantum-mechanical system, a discrete spectrum, so the energy can take only discrete values, which is typical for the energy levels in an atom. Thus, in the solutions of the known Schrödinger equation, ( in 1926 by the physicist Erwin Schrödinger asserted) the eigenvalues of the allowed energy levels of the electrons and the eigenfunctions of the corresponding wave functions of the electrons dar. The impossibility of simultaneous precise measurement of certain variables (eg of position and momentum ), as expressed by the Heisenberg uncertainty principle, is ultimately due to the fact that for the respective operators no common system of eigenvectors exists.