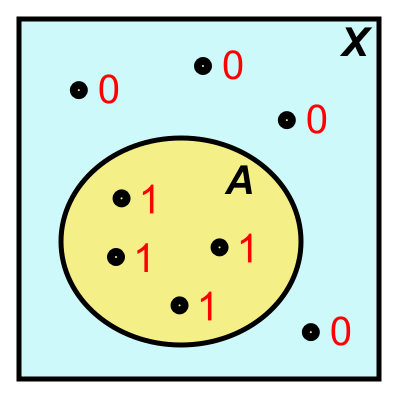
Indicator function

The characteristic function (also called indicator function ) of a subset of that referred to in the mathematical function by which is precisely when element of, and otherwise

The notations and are also common.

The assignment gives a bijection between the power set and the set of all functions of the amount

In the formation of the partial amount characteristic function is limited to the definition; in the sense of partial functions they can be thus described as follows:

Expected value, variance and covariance

For a given probability space and the indicator function is defined by if and otherwise is a random variable. For them, the following applies:

We see that the variance of is maximum in the case and two indicator variables are uncorrelated if and only if the associated events are stochastically independent.