Pairing function

The Cantor pairing function (sometimes numbering function) is an illustration used among others in theoretical computer science, which is based on the diagonal argument of Cantor.

With it, you can represent any pair of natural numbers by a single natural number. So you numbered all pairs of numbers. This numbering is even clearly reversible. That is, one can determine the original number pair again from the number. Mathematically speaking, this means that the Cantor pairing function is a bijective total function.

The idea of the diagonal counting the set of all pairs of natural numbers goes back to Georg Cantor. The generalization of the Cantor pairing function of pairs of tuples is called the Cantor Tupelfunktion.

• 6.1 Implementation of the calculations in Java
• 6.2 Pascal program to calculate the inverse

• 7.1 Proof of the predictability of Cantor's pairing function
• 7.2 Proof of the predictability of the inverse function
• 7.3 Use of computability

Motivation

In theoretical computer science the Cantor pairing function or Tupelfunktion is used to back perform functions that have more than one parameter to functions that have exactly one parameter only, which simplifies many proofs significantly.

The reduction of a problem to a (possibly simpler ) already known issue is a proven proof technique, which is called reduction.

With Cantor's pairing function or Tupelfunktion can the predictability of k - digit number functions to reduce the predictability of single digit number functions. That is, one can restrict to the study of single digits when investigating the predictability of numerical functions and know that the results obtained for all (thus also for the multi-digit ) number applicable functions.

Basics

It is perhaps not immediately obvious that it is possible to encode any arbitrary combination of two numbers by a number: The set of all pairs of numbers seems to be much larger than the set of all numbers.

^    |. . . . . . . . . . . .    x x x x x x x x x x x x.    x x x x x x x x x x x x.    x x x x x x x x x x x x. ~   - xxxxxxxxxxxx -> = - xxxxxxxxxxxx ->    | 0    x as a two-dimensional set of points   Grid on the number line 1 The Cantor pairing function, however, shows that the two quantities are equal, because it establishes a 1:1 relationship, it is a bijection.

A lot of that can be bijectively mapped to the natural numbers, is called countably infinite; in particular, have the natural numbers themselves this property. The Cantor pairing function then shows that the set of pairs of natural numbers is countably infinite.

Definition

The Cantor pairing function is defined as

Being allowed to start the natural numbers with 0.

Shorthand notation:

Encodes the pair

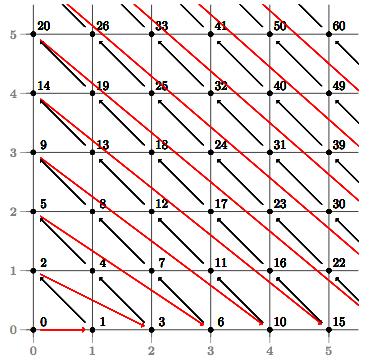
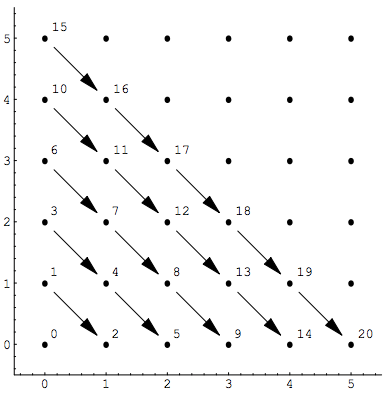
Here is a sketch of the diagonal counting:

On the axes, the two values ​​are plotted as a distance table suggests you the value of Cantor's pairing function in the intersection after, for example.

The numbering is quite simple: one diagonal with zero starting from the pairs: (0,0 ), ( 1,0), (0,1 ), ( 2,0), (1,1), (0,2 ), etc.

You can read the above education law directly, if the summation clear in each case over a column.

Extension to k-tuples

By repeated application also tuples can be clearly numbered. We define inductively the functions

Using the pairing function by:

And

The functions are called Cantor Tuple.

Shorthand notation:

Inverse function

The Cantor pairing function is reversible. The converse is clear and predictable. The latter is important for the application in theoretical computer science, as the predictability of the function and the inverse function is a requirement to represent all computable functions without problems by unary functions.

Reversible means that you can choose from a number n on the two numbers x and y are close, applies. The inverse function f consists of two auxiliary functions and q together:

Formal definition

We write its inverse as a component-wise, where:

Virtue of the projection

Which selects the i -th component of a tuple of length k.

In couples (the case) to write short and so that you can see the inverse of the pairing function as write.

With the auxiliary functions ( triangular number )

And

Or ( rounded triangular root )

And you can be calculated as follows for z:

And

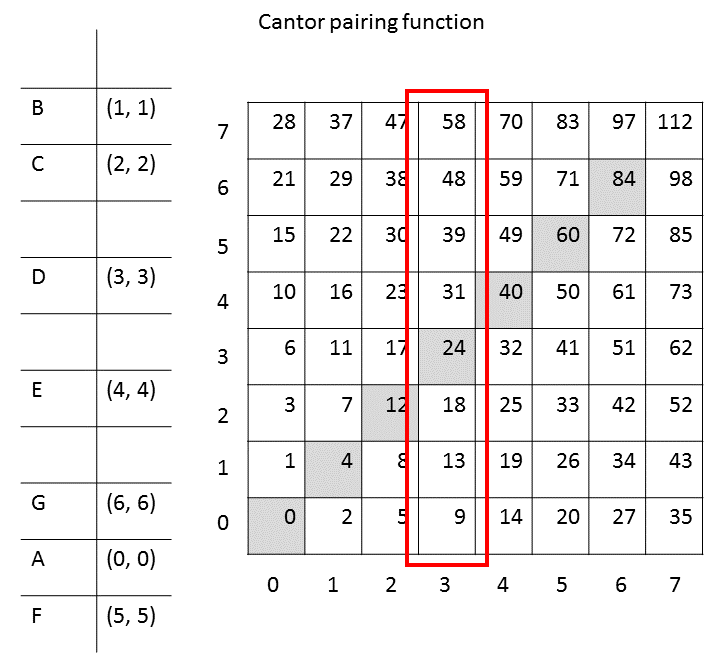
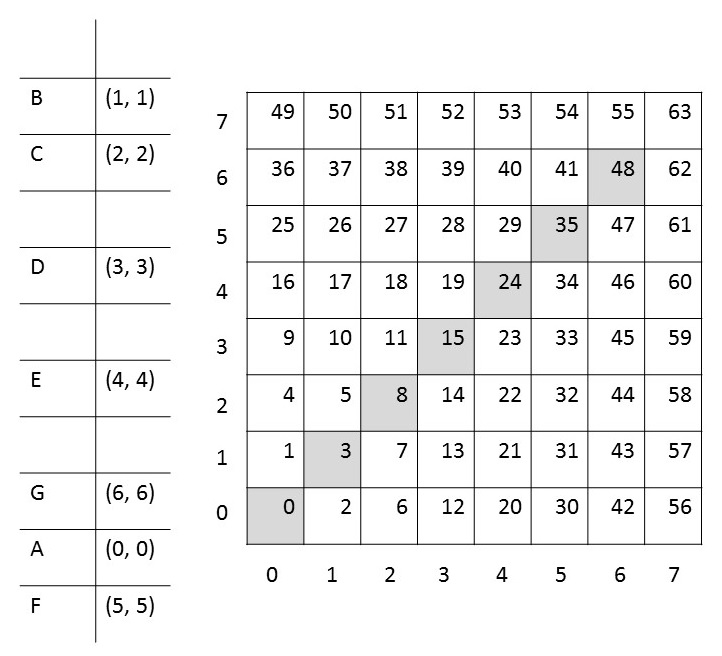
Example

Which pair of numbers represents the number 17?

For this first one determines the largest natural number w, applies. This can be either by trial and error to determine ( helps the values ​​of table ):

J 0 1 2 3 4 5 6   f ( j ) 0 1 3 6 10 15 21 or over the rounded formula of the triangular root:

Now you can use:

So is < 3,2 > = 17 That be based on the sketch above verify easily.

Computer implementations

Implementation of the calculations in Java

For large values ​​of z, the time requirement by the WHILE loop enormously, so has refrained from using loops and instead implemented the variant with the root triangle:

Public class Cantor {      public static long compute (long x, long y ) {        return ( x y) * (x y 1) / 2 y;      }      public static long Computex (long z ) {        long j = ( long) Math.floor ( Math.sqrt (0.25 2 * z ) - 0.5);        return y - (Z - j * (j 1) / 2);      }      public static long computeY (long z ) {        long j = ( long) Math.floor ( Math.sqrt (0.25 2 * z ) - 0.5);        return z - j * (j 1) / 2;      }    } The method compute calculates the given pair of numbers (x y ) assigned number, Computex and computeY are the inverse functions of computer.

Pascal program to calculate the inverse

The following Pascal program calculates the inverse function:

Procedure Cantor Pair (I: Integer; Var X, Y: Integer);   { Returns the i- th pair (X, Y) in Diagonalabzaehlung back }   var      J: Integer;        function F ( Z: Integer): Integer;      begin         F: = ( Z * (Z 1 ) ) div 2      end;        function Q ( Z: Integer): Integer;      var         V: Integer;      begin         V: = 0;         while F (v ) <= Z do            V: = V 1;         Q: = V - 1      end;     begin      J: = Q (I);      Y: = I - F (j);      X: = Y - Y;   end; Note: If the Pascal program is compiled on real machines, it must comply with the restrictions of real life computer. This means that for large values ​​of z integer overflows distort the result. For the view, however, a Pascal program is easier to understand than a register machine.

Predictability

The Cantor pairing function is a total, bijective, predictable ( even primitive recursive ) function, hence its inverse is computable.

Evidence of predictability of Cantor's pairing function

A method to prove that a function is computable, is to specify a register machine, which calculates the function.

This machine must be the function parameter x and passed in the register R1 in register R2 y. One then obtains the value of at the point (x, y) in the output register R0.

The following two-digit machine calculates the Cantor pairing function:

R4 = R1 R2; R5 = R4 1; R4 = R4 * R5; R4 = R4 / 2; R0 = R4 R2; At a formal proof that the register machine actually computes the function is omitted: This is obviously apparent when one compares the function rule to calculate the Cantor pairing function with the machine.

However, this register machine using commands that are not aware of the register machine simple. Simple register machine only knows the operations R 1, R-1 and the simple test.

By refining this register machine can however be attributed to a simple register machine.

Thus, there is a register machine that calculates the Cantor pairing function. Thus, the Cantor pairing function is computable.

Evidence of the predictability of the inverse function

For the proof of the inverse function, it is advisable to use a different definition of computability:

A function is computable if and only if a WHILE program exists that computes this function.

The above mentioned Pascal program can be refined to a WHILE program. Thus, there is a WHILE program, which calculates the inverse. Thus the converse is predictable.

Application of computability

From the predictability of the Cantor pairing function and its inverse follows that it is sufficient for the theory of computation, to deal with functions of single digits. For functions of the predictability then follows by applying the Cantor pairing function and its inverse function:

Computable iff there is a function g, with  ,    applies   and g is calculated. One can show for example that allows all rational numbers by an ordered triple ( i, j, k) represent. This predictability can be easily extended from the natural numbers to the set of rational numbers.

Origin

The idea comes from the set theory by Georg Cantor. He had the idea of ​​the magnitude of a quantity ( cardinality, cardinality) to compare with the size of another set, by trying to find a 1:1 mapping ( bijection ) of the elements of this set with the elements of the other set. Each element of the first set is to be assigned to exactly one element of the second set and vice versa. This seems complicated, but finds its justification when it comes to quantities with infinitely many elements. See also Galileo's paradox.

With a diagonal counting ( as indicated above) one shows easily that, for a countable set, the Cartesian product is to be equally powerful, which perhaps speaks against intuition, since tuples of different dimension occur.

Alternatives

There are many other ways to encode pairs of natural numbers bijectively by a natural number, for example, can be counted a little differently:

| 0 1 2 3 4 y   - ----------------------- >   0 | 0 2 3 9 10th   1 | 1 4 8 11th   2 | 5 7 12th   3 | 6 13th   4 | 14th     |.   x v The simple formula gives a bijection between and:

| 0 1 2 3 4 y   - ----------------------- >   0 | 1 3 5 7 9th   1 | 2 6 10 14 18th   2 | 4 12 20 28 36th   3 | 8 24 40 56 72nd   4 | 16 48 80 112 144.     |.   x v Evidence of reversibility: x is the largest natural number such that 2x a divisor of z, ie the number of factors of 2 in the prime factorization of such Let R = z/2x. Then y = (R-1 ) / 2

The prime factorization gives a way to encode arbitrary finite tuples of natural numbers by natural numbers:

Example: