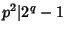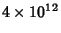Wieferich prime

A Wieferich prime number is a prime number p with the property that 2p - 1 - 1 is divisible by p2.

Alternatively, one can write this as congruence:

Such primes were described in 1909 by the German mathematician Arthur Wieferich first time.

Known Wieferich primes

We know so far only two Wieferich prime numbers, namely 1093 ( Waldemar Meissner 1913) and 3511 ( Beeger 1922). With the help of computers to November 2008, all numbers up to 6.7 × 1015 were examined, further Wieferich primes did not find you there. It is not known whether there are infinitely many primes Wieferich. It consists of both the presumption that this is not the case, as well as the opposite, more precisely, that lie between and about Wieferich primes. There is even an open question whether there are infinitely many primes that are not Wieferich primes. Joseph Silverman showed this in 1988, assuming the abc- conjecture.

Relationship with the great Fermat's theorem

Wieferich dealt with the great Fermat's theorem. In 1909 he published as a result of the sentence:

If xp y p cp = 0, where x, y and z are integers, p is a prime number, and the product x · y · z is not divisible by p, then p is a prime number Wieferich so 2p 1-1 divisible by p2.

1910 showed Dmitry Mirimanoff that then 3p - 1 - 1 is divisible by p2. The only known prime numbers that satisfy this condition are p = 11 and p = 1006003 ( Kloss 1965).

It follows from the 1995 proved Fermat's great theorem that the hypotheses of Wieferich can not be met.

Properties of Wieferich primes

• From Wieferich prime w is the Mersenne number Mn can be = 2w -1 -1 constructed as a product w -1 = k · w2 = w -1.

• It is an open question whether there < w -1 ( with prime exponents p) are Mersenne numbers Mp, which are divisible by w2. It must p is a divisor of w -1 be if Mp should be divisible by w.

• Unlike other bases than 2: for other bases than 2, and the corresponding equivalents to Mersenne and Wieferichzahlen this is not true.

• For a Wieferich prime p is true:

• With 2n ≡ 1 (mod p) always occurs at the same time 2n ≡ 1 (mod p2) on.