AVL tree

The AVL tree is a data structure in computer science, namely a binary search tree with the additional property that the height of the two subtrees differs by at most one at each node. This property makes it a balanced binary search tree, that is, its height grows only logarithmically with the number of keys. Likewise logarithmic behaves the maximum number of steps ( comparisons) that are necessary to determine the presence or absence of a key, and the maximum cost for operations for inserting and removing a key. Although the latter change the AVL tree, but the result is again an AVL tree.

The AVL tree is named after the Soviet mathematicians Georgi Maximowitsch Adelson - Velski and Yevgeny Mikhailovich Landis, who introduced the data structure in 1962. Thus the AVL tree is the oldest data structure for balanced trees.

• 4.1 Single rotation in AVL tree
• 4.2 double rotation in AVL tree
• 4.3 Example

• 5.1 chaining
• 5.2 columns
• 5.3 Application Examples

• 6.1 head
• 6.2 Iterative programming
• 6.3 Separation of navigating by the modifying operations
• 6.4 cursor
• 6.5 Example of an application with multiple AVL access paths
• 6.6 parallelization

Motivation

Search trees are solutions of the so-called " dictionary problem." Adopted, a large number of keys, which a value is added to each. In a dictionary German - English the German word is the key and English words are of value sought. Similarly, in a directory with names and address as the key and the phone number as the search value.

Mathematically realized a dictionary a (finite ) function with pairs ( key, value ). When searching a keyword (argument of the function) is associated with a key to the cover. Does this success, the search term, the corresponding value is assigned as the function value.

In both examples, usually the keys are ordered. This is very useful because it allows to pitch the book in the middle and to check whether the search string is found. If it is not found and example, it is alphabetically before the letter "K", you know, in addition, that one must not compare with the rear "L", "M" or "Z". The remaining part of the examination is always a contiguous segment, which, like the whole book is halved again at the beginning - and so on to the Fund or to determine is that the search term is not found.

This procedure has been in the computer science called " binary search ". It is modeled in an obvious way by the well-known search techniques " binary search in the array ." Their behavior is information-theoretically optimal, namely, logarithmic, or more precisely the case of n keys one needs a maximum of log2 ( n 1) comparisons.

Unlike the binary search in the " sequential search" the search term must be potentially compared with all keys. ( For this, however, needs the input to be not sorted. ) The difference between the two methods can be substantial: in a phone book with n = 220-1 = 1'048'575 entries must for sequential Search in means ( 1048575 1) / 2 = 524'288 comparisons are performed. When binary search can be reached after a maximum of log2 ( 220) = 20 compare to the same result.

Changes, additions and disposals of words and phone books can sporadically in software systems, they must be immediately reflected in the rule. Additions and disposals require in an array data transports, their effort, ie linear in n, is proportional to the length of the array. Such costs represent the efficiency of binary searching destroyed completely.

The procedure for binary search can be modeled with a binary tree. The first key with which the search term is to be compared is placed in the root of the binary tree. The aufzusuchende the comparison result "lighter" next key is placed in the left child node - according to the key for "greater" in the right child node. So it continues until all keys are stored in the binary tree. (This is the binary tree to a binary search tree. )

By removing the individual elements of the array flexibility is obtained: The effort when inserting for assigning storage space and loading the fields with values ​​and deleting for the return of the memory space is independent of the number n of elements. Is lost in the binary tree, however, a measure of the balance, which is optionally in the array by forming the mean value between the two indexes. In addition, a binary tree, which was once poised excellent, losing by insertions and deletions his balance and, in extreme cases, namely when each node only one child node ( instead of two), degenerate into a linear list - with the result that a search a sequential search is tantamount.

Computer scientists have developed various balance criteria for binary trees. In most of the efforts for the search, insert, and delete are logarithmic, albeit with different constant factors.

When AVL tree, the balance is defined by the height, he is a height- balanced binary search tree. Other solutions to the problem of degeneracy in dynamic binary trees can be found in

Definition

When the balance factor BF (t ) of a node, respectively. Subtree [NB 1 ] t in a binary tree is defined as the difference in height

Where H ( t) is the height of the tree t, and tl is left, tr the right child tree of t.

A binary search tree is then just an AVL tree if there are precautions that compliance with the AVL condition

At all its nodes t sure.

This definition limits the height H (t ) of an AVL tree t with n nodes by the inequality

With c: = 1/log2 Φ ≈ 1.440420, b: = c / 2 log2 5 - 2 ≈ -0.327724 and Φ: = 1 √ 5/2 ≈ 1.618034 ( number of the golden ratio ).

The lower bound comes from the fully balanced binary tree (which to the lowest level, all levels are complete); the top of the Fibonacci tree representing an AVL tree with the smallest number of nodes at a given height, is thus poised at worst. [NB 2]

Operations

The most important operations in the search trees - and thus the AVL tree - are: Retrieving one hand, and inserting and deleting the other. The navigation operations, which are the various search operations, the traversal, searching first or last element and the like, let the tree unchanged and basically work on any binary search tree.

With the characteristic that all of these operations in the worst case have (worst case) logarithmic complexity, the AVL tree is one of the height -balanced binary search trees.

Search

The Search (english: find, search or locate) an element by its key is the most important of the navigation operations. The height - balancing of the AVL - tree tries to optimize this operation down. It allows a so-called direct access (as opposed to sequential access of the traversal ). It is generally used as a preliminary operation both when inserting and deleting.

The binary search tree is always sorted so that the left of each node, only nodes with smaller ( or the same) keys, and right nodes are stored only with larger (or equal ) keys. For this to work, the available user-supplied comparison function must return a total ordering (more precisely: the total quasi-ordering ) establish. In the comparison function puts the specification of "key". We therefore find a keyword by travels from the root of the tree in layers down and be branched to the left if the search term is smaller than the key of the current node, or to the right if it is greater. Conforms a key, then the search is successful. When you reach a node whose key does not match and in the required direction of a successor ( child ) is missing, it is guaranteed that the key does not exist in the tree (see Search free of duplicates ). In this case, the search is not successful. The result is the last node compared with the last studied direction, which are returned to the user both, so he can use them as needed as the insertion point.

Both duplicate free as well as trees with duplicates ( elements with the same keys ) can be implemented. ( This is less a question of the comparison function as one of the application. ) In the latter, a search operation is attached, which is always up to the ( semi-) leaves (which are nodes with out-degree 0 or 1) down searches, and allows an element targeted according insert on the application scenario either the left of the left-most ( left-most ) or the right of the rightmost duplicate. With such a search operation, the existing order of elements can be preserved with the same key ( or exactly vice versa). Is, for example, together with the insert operation of a sorting part of the algorithm, then these "stable" (see Stability ( sorting process ) of explanatory examples). For implementation see Searching with duplicates.

In all variants of the complexity in both the agent and in the worst case is logarithmic. The sorting a mass of n elements by repeatedly searching and inserting costs n -log -n, ie no more than with the best sorting method.

Traverse ( iterate, enumerate )

The in -order traversal, which means navigating both to the left and to the right to the next neighbor in the given sort order is particularly useful when a single operation, as a cross- step, is present. Thus, the user can set up a loop in the usual manner: Start with the search operation (or the first element ), iteration with the Traversieroperation.

The transverse step has on average constant and in the worst case logarithmic cost. In a traversal over the tree, each edge of the tree is exactly one descending and ascending once visited.

Prospect for the first or last element

Related herewith is the positioning of the smallest or largest element in the tree, which behaves logarithmically in both the means as in the worst case.

An interval concept ( both actually as inauthentic ) leaves over the totally ordered set of elements in the tree be realized as a kind of " fuzzy" search, namely by "heavier" or "lighter" (see binary search tree ( Proximitätssuche ) ) - also with logarithmic effort.

Insert ( Add )

It is assumed that the navigation is carried out already at the insertion point. An insertion point is an external node and the far left or far right, or between two internal ( and key supporting ) node, so it can definitely by an (internal ) node, together with a direction ( left or right) to be specified. The nodes are far left or far right always (half) leaves, as well as two neighboring nodes always a ( semi-) is exactly one leaf. Such a node is - together with the appropriate direction - referred to as the direct insertion point. He is also supplied by an unsuccessful search operation.

To insert (english: insert or add) the node hooked with the new key as a leaf at the insertion - in other words, the external sheet is for internal sheet. The height of the existing of this sheet subtree increases from 0 to 1 the ascent to the parent node, there corresponding to the three values ​​of the original balance factor of the parent node 3 options for the new (temporary) balance factor:

The insertion of the ( n 1 ) th node in an AVL tree with n nodes has the worst-case logarithmic cost, for example, if each level needs to be checked all the way up to the root. However, since this probability from level to level upwards decreases exponentially, the need for inserting in the middle is constant. [NB 3] This is not counting the exploration of the insertion point.

Delete ( delivery, removal )

Navigation to the node to be deleted can be done by means of a search, but also by a transverse step. When deleting (English: delete or remove) are more cases to distinguish than when pasting (see binary tree ). Simple are the cases where the node to be deleted is a ( semi-) leaf. But if he has two children who both released subtrees must be re- suspended. Then, click on one of the in -order neighbors, so either the rightmost node of the left subtree or the leftmost of the right subtree (of the two subtrees can should higher preference ) to it to hang the two subtrees again. The required maximum descent goes through so many steps, such as the height, and on average exactly one. The replacement node is latched in the hierarchy of the tree at the location of the deleted node, but has to be self- removed from its home subtree - that's just because he's a (half) sheet (see binary tree ).

Because ultimately, in any case, an internal sheet is removed as a child node to its height decreases from 1 to 0 the ascent to the parent node, there corresponding to the three values ​​of the original balance factor of the parent node 3 options for the new (temporary) balance factor:

The cost for deletion is in the worst case, logarithmic ( with or without the search); but on average, if you do not count spotting the deletion candidate, he is constant, since the probability for the need to have to check the balance on the next higher level, upwards decreases exponentially. [NB 4]

Rebalancing

If during surgery the AVL balance is lost, that is a height difference of more than 1 between two sibling subtrees arises a rebalancing must be done. This must be (hence the characterization as in English self -balancing tree ) done within the function called "automatic". Suitable repair tools are the so-called rotations.

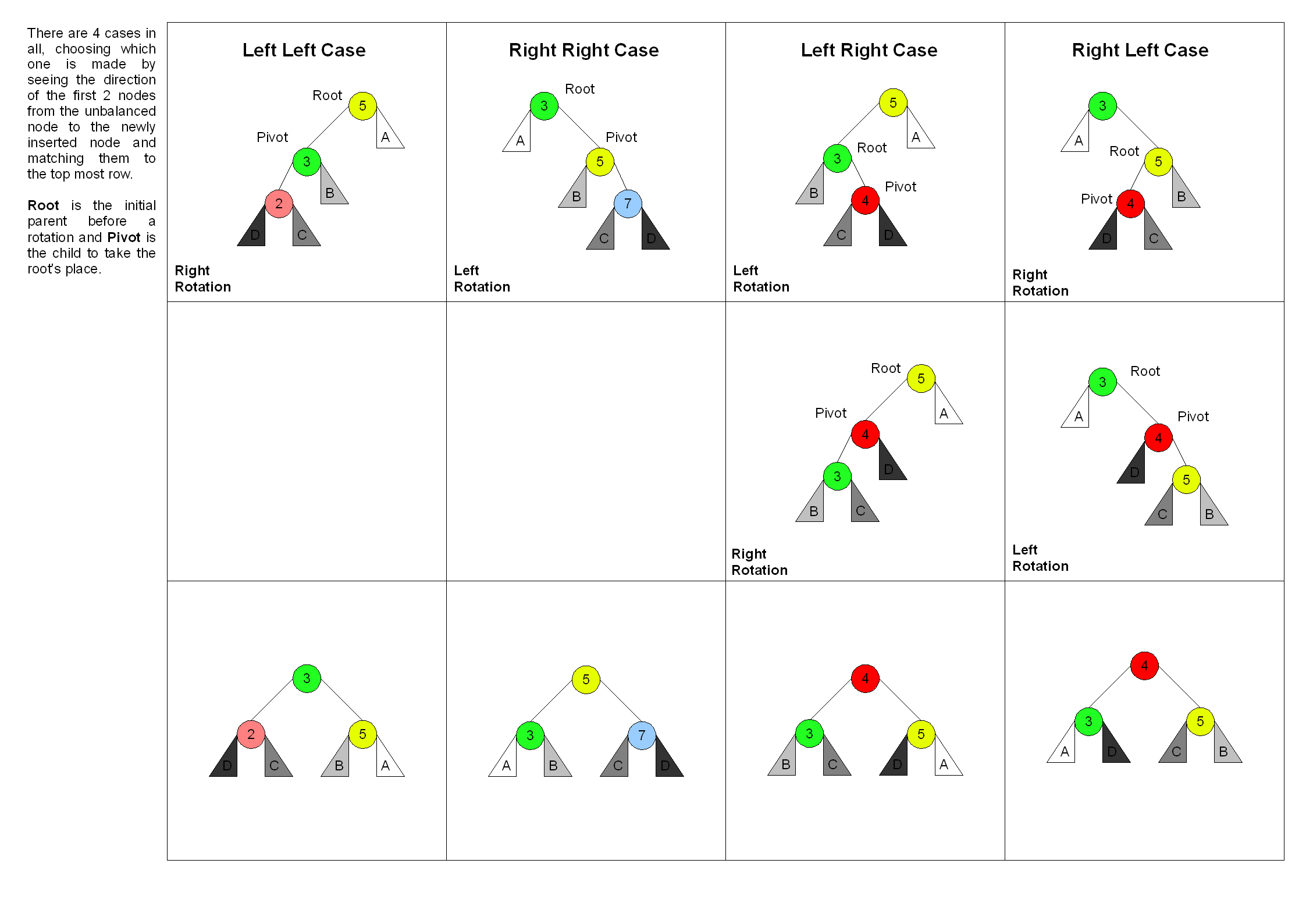
For insertions and deletions, in which the temporary height difference never exceeds 2, two variants are needed: single and double rotation. A single rotation makes the rebalancing when the inner child of about 2 higher sibling (Z in the two Figures 2 and 3 ), which is the child with a child's direction is the opposite of Z, ( t23 in Figure 2 and Y in of Figure 3) is not higher than its sibling, the outer child (t4 in both figures ). This case is ( resp. mirrored in the literature as a right-right - left-left ) situation referred to as X to the right and Z is left -heavy, that is, the two balancing factors 2 and 1 ( when deleting and 0) are in short, the balance after the other has the same direction twice. The other case in which the inner child is higher, is covered by a double rotation - in the literature left-right (or left-right ) situation called because X to the right and Z is left -heavy, that is, the two balance factors 2 and -1 are, in short, the balance changes direction.

The principle of rotation in the binary trees is described with reference to Figure 2. A single rotation can be specified by the direction of rotation left or right and through the root of the subtree affected, for example, links (X). It causes the lowering of this X and the raising of another node ( here: Z). Overall, it comes to the following three actions:

In short: a rotation " wobbles " an edge ( here: X → Z) of the tree in their different orientation ( Z → X). For this purpose, the necessary adjustments to the two incident nodes come ( here: X and Z).

The key move in these " rotations " only vertically ( within the vertical height). The in -order sequence of nodes that indeed reflects the sort order, so stay perfectly preserved.

Rotation comprises only a constant number of link changes to a constant number of nodes.

Easy rotation in AVL tree

It is called in the original Малое вращение (small rotation).

The above Figure 2 shows a right-right situation. In the upper half of the two subtrees t1 and Z of the node X has a height difference of 2 The inner child have t23 of about 2 higher node Z is not higher than its sibling t4. This can occur after insertion in the subtree t4 or after a deletion from the subtree t1. The in Figure 2 pale -held case that t23 as high as t4, only occurs when deleting.

The rebalancing (shown in the lower half of the figure) can be achieved by a single rotation to the left. It is already described above as a single rotation. Adjustments to the 3 threads are drawn increasingly into the picture.

The height of the new subtree Z is the same for an insertion of the X before the operation while it is decreased or unchanged in the deletion by 1, depending on whether Z was right skewed or not.

The mirrored, the left-left situation is handled by a single rotation to the right.

Double rotation in AVL tree

It is called in the original Большое вращение (large rotation).

The situation shown above in Figure 3 differs in that the middle subtree ( with root Y), which is the inner child of about 2 higher node Z is higher than its sibling t4 from that in Figure 2 - a right-left situation, since X to the right and Z is left -heavy. This can happen after an insert in one of the subtrees t2 or t3 or after deletion of the subtree t1. The in figure 3 held in standard color case where t2 as high as t3 occurs only when deleting, while the 2 height dissimilar cases (exactly one subtree pale ) both occur when inserting to deleting. The fourth case (twice pale ) requires no rebalancing.

The double rotation, the result of which is shown in the lower third of the figure, followed by a left rotation by X ( against the Rechtslastigkeit of X) is a right rotation by Z ( against the leaning to the left of Z, middle third ). It causes a twofold increase in the higher ( and inner) child Y of Z

Adjustments to the 5 threads are drawn increasingly into the picture.

The height of the new subtree Y is the same as that after insertion of X prior to the operation, while it is reduced by deletion of 1.

In a left -right situation is the mirrored version, that is a rotation to the left followed by a right rotation needed.

Example

The AVL tree in Figure 1 is

• After the deletion of the node G by the two single rotations law ( F), later left ( J)
• After the insertion of a node T by the double rotation right links (V, P)

Rebalanced.

Operations with whole AVL trees

Concatenate

Two AVL trees can be concatenated with a logarithmic expense ( concatenated ) to (English: concat or even cat). Of course, must precede all the keys of the second all the keys of the first tree for the sort order. [NB 7]

Cleave

Somewhat more complicated than concatenating the columns (English: split ) an AVL tree in two separate AVL trees to an external node, ie a point between two internal nodes ( keys), which as a pair ( node, direction) including the path is given to the root. To the left of the left partition is with the smaller keys and the right, the right one with the larger ones. The so specified separation line ( red in Figure 5) cuts edges of the given tree on the path of the node to the root, so that left and right a forest of " snippets " results. Finally, each of the two forests can be combined with a logarithmic overhead to an AVL tree. [NB 8]

Application Examples

The mass extinction of all keys in an interval can be done by double columns and unique concatenating or if the smallest or largest element is part of it, by a single column.

A mass insertion can be performed by a single column and concatenating twice as long as the amount is prepared as an AVL tree and their keys are in an interval that is not found in the target tree.

Implementation

In addition to the requirements of the binary search tree must be placed in a node of the balance factor with its three values ​​: makes 2 bits [NB 9].

Head

Since the root of a deletion or a rotational fall prey to, so the tree can not represent, should this role be of a different data structure adopted, which is in the literature called head. It contains the pointer to the root and acts as a parent of the root.

Iterative programming

In the literature, the operations are often presented in a recursive programming. However, the user has several advantages thereof if the implementer has the elegant of writing down her recursions replaced by simple iterations, as this h (height) procedure calls and returns jumps are saved and the memory required for the program stack is kept constant. But it's not just about conserving resources. When Traversieroperation thus for example, the programming of the application is greatly simplified. For the storage of the way back to the root and head, which is used for modifications to adjust the balance factors, but also when traversing and unplugged during the recursive programming among other things in the program stack, then you have another, are chosen explicit construct to the cursor (see below) can be subsumed. This separation of the modifying operations of the navigation is possible.

Separation of navigating by the modifying operations

Insert and delete operations are usefully be separated from the search operation, albeit in a different manner than the standard search operation to navigate to the insertion point, or node, for example by means of a cross- step, or by using a second search structure for the same element as in # example of an application with multiple AVL access paths.

This modularization of sets navigation of the modifying operations to unterlogarithmischen in the middle (read: constant ) cost of the latter free, for a climb up to the root (as in [NB 3] and [NB 4] shown ) is required only in exceptional cases. In applications with high sequential proportion could the positive impact on the runtime.

Cursor

When looking for a pair (node ​​, direction) is generated, which is suitable to specify the insertion point when you insert. When deleting the node to be deleted is indicated by the component nodes, and specifies the direction component, where the cursor should proceed after the deletion. When traversing nodes are the starting point and the direction of the desired direction of navigation Nails to come back with such a pair in the result. To produce and / or consume all important operations a construct that is called ( in analogy to example to the databases ) cursor.

The size of the cursor depends crucially on whether the AVL nodes contain a pointer to the parent or not.

In all operations, access to the parent node on the stack in the cursor is slightly more expensive than the parent pointer. If the path be held valid in the cursor after a modifying operation ( for example, for sequential insertions or deletions ), nor is an additional percentage added (on average constant and at worst logarithmic ) surcharge. This may be so but are provided only for a cursor, the input cursor. Requires an application uses multiple cursors for the same search tree and changes to it away, then maintaining the consistency of the cursor stack can (for example, by re- search with logarithmic on average costs) are so complex that it is more economical, the tree parent pointer to donate.

Example of an application with multiple AVL access paths

As an example of an application with two access paths a classic memory management is taken. Elements of the data structure are the free memory blocks with attributes (fields) size and location. For each of the two fields there is a search structure. When acquiring a block is wanted from minimum size, discharged and entered a possible rest again. In the memory return to search for place checked for conflict with the freedom of neighboring blocks ( also an example of the utility of the cross- step), where appropriate, and the fused block to be returned thereto. All changes must be pulled on both search structures. Are parent pointer exists, then saves the hand over hand from a search structure to the other one search.

Parallelization

If iteratively programmed, then the inspection and repair loop in the reverse direction, ie from the head and root to leaf, are passed through. This is particularly interesting when highly parallel to the tree ( competitor ) to be accessed. For example, the search operation would be in a scenario " Search -and-paste " is the lowest (last) unbalanced node noted on the path from that tree there to lock [NB 11] and store the comparison results. Would then have to complete the insert operation, the locked ancestor ( possibly after a rebalancing ) to balanced and all his descendants are set to the leaf on which the chosen directions corresponding balance factors. The advantage would be that all nodes could be consistent visited outside the restricted subtree of the other processor cores running parallel to the insertion and also changed.

Compared with red-black tree

The amount of AVL trees is a proper subset in the set of red -black trees. For every binary tree which is in the form of AVL, red - black - criterion fulfilling way can be in a Mercator projection. [NB 12] However, there are red-black trees are not AVL - balanced. The graph alongside shows, for example, a red-black tree with 6 (inner) node and the external path length sum of 21, while 20 the largest external path length sum in AVL trees (and also the smallest of all binary trees ) of this size. Consequently, the worst case amount of the AVL tree is smaller than that of the red-black tree, namely by a factor c / 2 ≈ 0.720. In general, the search time behavior of the AVL - tree is considered to be favorable.

The space requirement is virtually identical: 1 bit for the color compared to 2 or even 1 bit ( s ) [NB 9] for the balance factor.

The space requirement and the runtime behavior for the described operations behave identically in the middle and in the worst case. While offering the red-black tree amortized constant modification costs and the AVL tree only in the central constant [NB 13] applications of binary search trees, the only sequences of insertions and deletions -. , But no intervening search operations - contain, use the purpose of the search tree not enough. So you see this kind of applications from, the overall behavior of a mixture of searching and modification is amortized in two data structures, logarithmic in the middle and in the worst case.

Realistic situations with application performance data and comparing - also with other search algorithms and varieties of data structures - can be found at Ben Pfaff. His results show in 79 measurements, among others, the very great similarity of AVL trees (AVL ), and red - black trees ( RB) with runtime conditions AVL / RB 0.677 to 1.077 with a median of ≈ 0.947 and a geometric mean value of ≈ 0.910.

Applications

As Ben Pfaff shows that dynamic search trees AVL tree, red-black tree and splay tree cover the same essential functions. Large differences he notes, in the run-time behavior, the AVL tree in the median and mean scores best.

In computer science, the dynamic search tree structures have a wide range of applications as a basic tool in:

• Duplicate suppression, deduplication, duplicate detection
• Elementary set operations such as averaging and association
• Standard Template Library (STL )

At Ben Pfaff to low-level applications are (all x86 -based Linux):

• Management of Virtual Memory Areas ( VMAs ) including range of queries to determine the overlap of existing VMAs (p. 4)
• Clear marking of IP packets (p. 7)

In addition:

• List of variables in a program that has to care for an interpreter: the interpreter must at all times be able to decide whether a program variable is assigned a value currently and if so, which. The same applies to a compiler.
• In section # Locate the "Sort by inserting ".
• In section # example of an application with multiple AVL access paths a classic memory management.

Historical

The section # motivation mentioned, very well-known search tree Binary search in the array is considered the forerunner of the dynamic search tree structures. An obvious implementation of the lookup in a ( sorted) dictionary, they may have been developed and implemented several times and without knowledge of other implementations. However, in dynamic application, they can not keep up with the newer developments, although it is an excellent solution in the static case. There are macros that cause a compiler to generate code for a loop-free binary search for a given table of ( key, value ) pairs.

In 1962 appeared for the first time a dynamic search tree structure in the form of the AVL - tree. Its inventors are the called Soviet mathematician Georgy Adelson - Welski and Yevgeniy Landis. Her contribution to the journal Doklady Akademii Nauk SSSR was translated into English in the same year. Translation is ( as according to the original) the very ambitious title "An algorithm for the organization of information". The name AVL tree is not found in this translation.

In 1970, Rudolf Bayer published his first work on the B-tree. He is not a binary tree, supports heterogeneous storage, such as main memory and backing store, and is used in database systems.

This was followed in 1972 under the name "symmetric binary B -tree " of the red-black tree of Rudolf Bayer. He had the balance control of the AVL - tree too strict. A name was changed in 1978 by Leonidas Guibas and Robert Sedgewick in the now common "red -black tree", and later "RB tree".

Splay trees were introduced in 1985 by Daniel Sleator and Robert Tarjan under the name " Self-Adjusting Binary Search Trees". They are more dynamic than those indicated above, by also changing in search operations.

A rough comparison of dynamic search trees can be found in

For more information